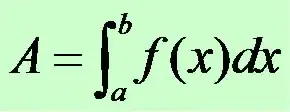I have 1200 data samples of amplitude data over a 5-minute period, with 4-5 "spikes" in the data. These can be nearby to each other, so "shoulders" can appear. The data can be somewhat noisy as well.
I need to:
- Programmatically determine the times where these peak occur, and
- Ultimately determine the integral of the curves to find the area under each discrete peak, ignoring the amplitude from nearby neighbors.
The latter requirement makes me think I need to derive a function for each component, and use that function to calculate the area beneath.
Is this a Discrete Wavelet Transform problem? Fourier Transform? Short-time Fourier transform? Something else? Is there a Java library to help with this?
I'm looking for a way to determine the 5 equations that, when added together, yield the original data curve. Probably something like these Gaussian curves (which I just eyeballed)