Python: Fitting a piecewise polynomial

Question

I am trying to fit a piecewise polynomial function

Code:

import numpy as np
import scipy
from scipy.interpolate import UnivariateSpline, splrep
from scipy.optimize import curve_fit
from matplotlib import pyplot as plt


def piecewise_func(x, X, Y):
    """
    cond_l: condition list
    func_l: function list
    """
    spl = UnivariateSpline(X, Y, k=3, s=0.5)
    tck = (spl._data[8], spl._data[9], 3)  # tck = (knots, coefficients, degree)
    p = scipy.interpolate.PPoly.from_spline(tck)

    cond_l = []
    func_l = []
    for idx, i in enumerate(range(3, len(spl.get_knots()) + 3 - 1)):
        cond_l.append([(x >= p.x[i] & x < p.x[i + 1])])
        func_l.append([lambda x: p.c[3, i] + p.c[2, i] * x + p.c[1, i] * x ** 2 + p.c[0, i] * x ** 3])

    return np.piecewise(x, cond_l, func_l)


if __name__ == '__main__':

    xdata = [0.28190937,  0.63429607,  0.91620544,  1.68793236, 2.32350115,  2.95215219, 4.5,
         4.78103382,  7.2, 7.53430054,  8.03627018,  9., 9.86212529, 11.25951191, 11.62658532, 11.65598578, 13.90295926]
    ydata = [0.36273168,  0.81614628,  1.17887796,  1.4475374,   5.52692706,  2.17548169, 3.55313396,  3.80326533,  7.75556311,  8.30176616, 10.72117182, 11.2499386,
        11.72296513, 11.02146624, 14.51260631, 20.59365525, 21.77847853]

    spl = UnivariateSpline(xdata, ydata, k=3, s=1)

    plt.plot(xdata, ydata, '*')
    plt.plot(xdata, spl(xdata))
    plt.show()
    
    p, e = curve_fit(piecewise_func, xdata, ydata)
    # x_plot = np.linspace(0., 0.15, len(x))
    # plt.plot(x, y, "+")
    # plt.plot(x, (piecewise_func(x_plot, *p)), 'C3-', lw=3)

I tried the UnivariateSpline function to interpolate, I see the following result

However, I don't want the polynomial curve to pass through all data points. I tried varying the smoothing factor but I am not able to obtain something like the one below.

Expected output:

I'm trying curve fitting (Use UnivariateSpline to fit data tightly) to get the expected output and I have the following issues.

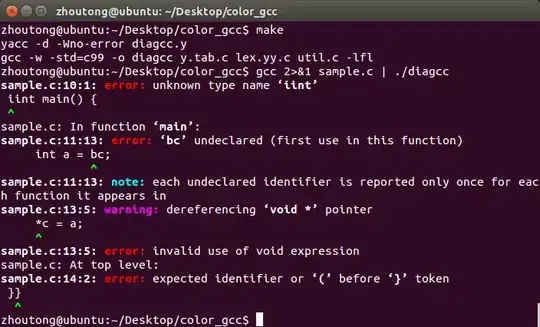
piecewise_func in the code posted returns the piecewise polynomial. Passing this to curve_fit(piecewise_func, xdata, ydata) returns an error

Error: res = leastsq(func, p0, Dfun=jac, full_output=1, **kwargs) ValueError: diff requires input that is at least one dimensional

I am not sure what is wrong.

Suggestions on how to get the expected fit will be of great help.

Answer 1

I would recommend having a closer look at the parameter s in the UnivariateSpline documentation:

s : float or None, optional

Positive smoothing factor used to choose the number of knots. Number of knots will be increased until the smoothing condition is satisfied:

sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s

If s is None, s = len(w) which should be a good value if 1/w[i] is an estimate of the standard deviation of y[i]. If 0, spline will interpolate through all data points. Default is None.

Since you do not set w, this is just a complicated way of saying that s is the least squares error that you allow, i.e., squared errors summed over all the data points. Your value of 1 does not lead to interpolation but it is quite tight compared to what you want to achieve.

Taking

    spl = UnivariateSpline(xdata, ydata, k=3, s=10)

you get the following:

Yet closer to your goal is s=100:

So my recommendation is to play around with s and if that proves insufficient, to ask a new question describing what you need more precisely. I haven't had a proper look at the problem with piecewise_func.