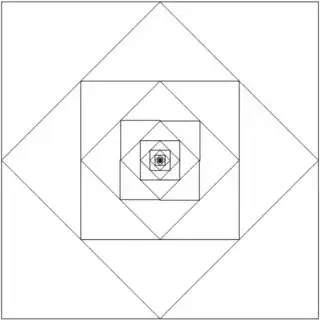
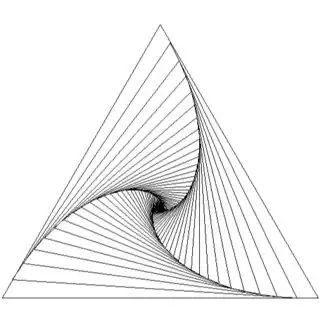
I'm trying to recreate this image using Python and PIL.
This is the code I come upped with:
from PIL import Image, ImageDraw
def draw_lines(draw, points):
new_points = []
for idx, point in enumerate(points):
x, y = point
if idx != len(points) - 1:
if idx == 0:
x = x + 25
elif idx == 1:
y = y + 25
elif idx == 2:
x = x - 25
elif idx == 3:
y = y - 25
else:
x = x + 25
new_points.append((x, y))
draw.line(new_points, fill="black", width=1)
return new_points
def main():
im = Image.new('RGB', (501, 501), color=(255, 255, 255))
draw = ImageDraw.Draw(im)
points = [
(0, 0),
(500, 0),
(500, 500),
(0, 500),
(0, 0),
]
draw.line(points, fill="black", width=1)
for i in range(80):
points = draw_lines(draw, points)
im.save("out.png")
if __name__ == '__main__':
main()
and this is the output:
and also how can I fill those formed triangles with color?
Update:
By modifying the answer here Rotating a square in PIL, I was able to do this.
Code:
import math
from PIL import Image, ImageDraw
def distance(ax, ay, bx, by):
return math.sqrt((by - ay) ** 2 + (bx - ax) ** 2)
def rotated_about(ax, ay, bx, by, angle):
radius = distance(ax, ay, bx, by)
angle += math.atan2(ay - by, ax - bx)
return (
round(bx + radius * math.cos(angle)),
round(by + radius * math.sin(angle))
)
image = Image.new('RGB', (510, 510), color=(255, 255, 255))
draw = ImageDraw.Draw(image)
def draw_sqr(pos, sqlen, rota):
square_center = pos
square_length = sqlen
square_vertices = (
(square_center[0] + square_length / 2, square_center[1] + square_length / 2),
(square_center[0] + square_length / 2, square_center[1] - square_length / 2),
(square_center[0] - square_length / 2, square_center[1] - square_length / 2),
(square_center[0] - square_length / 2, square_center[1] + square_length / 2)
)
square_vertices = [rotated_about(x, y, square_center[0], square_center[1], math.radians(rota)) for x, y in
square_vertices]
draw.polygon(square_vertices, outline="black")
def draw_rot_sqr(pos):
scale = 500
rot = 0
n = 1.1575
for i in range(10):
draw_sqr(pos, scale, rot)
rot = rot * n + 10
scale = scale / n - 10
draw_rot_sqr((255, 255))
image.show()
Now, how can I properly scale and rotate the squares where all points intersect with the sides at any size?
Edit, drawing triangles
Vertices for drawing triangles:
def draw_sqr(pos, p_len, rota):
x, y = pos
altitude = p_len * math.sqrt(3) / 2
apothem = altitude / 3
x_top = x
y_top = y - apothem * 2
x_base_1 = x + p_len / 2
x_base_2 = x - p_len / 2
y_base = y + apothem
vertices = (
(x_top, y_top),
(x_base_1, y_base),
(x_base_2, y_base)
)
vertices = [rotated_about(x, y, pos[0], pos[1], rota) for x, y in
vertices]
draw.polygon(vertices, outline="black")



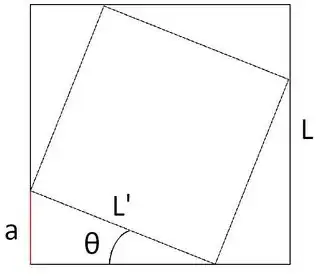
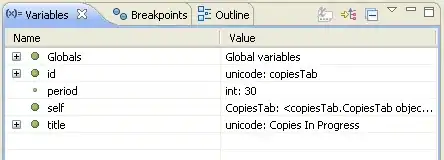 is the length of the sides of the starting square, and
is the length of the sides of the starting square, and 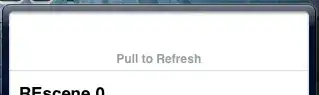 is the length for the new square, we must find
is the length for the new square, we must find  such that, when rotating the new square by it, all corners touch the sides of the previous square.
such that, when rotating the new square by it, all corners touch the sides of the previous square. , in which
, in which 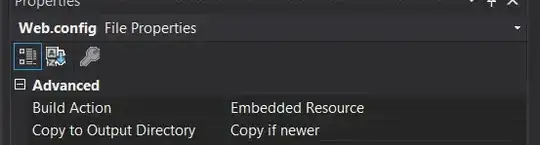 is the scaling factor. For example, if the scaling factor is 0.9, each new square's sides will be 90% of the length of the sides for the previous one.
is the scaling factor. For example, if the scaling factor is 0.9, each new square's sides will be 90% of the length of the sides for the previous one. 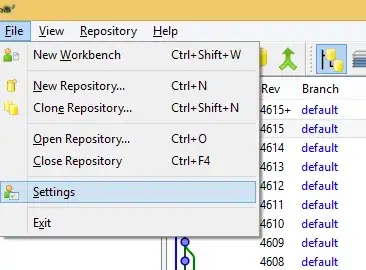 can be found to be:
can be found to be: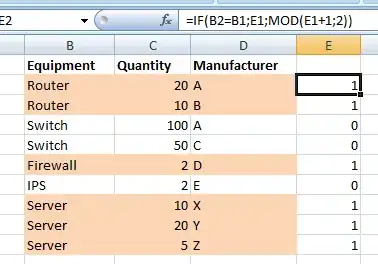

 should be no smaller than the sides of the previous one, which translates to
should be no smaller than the sides of the previous one, which translates to  .
. 
 scaling factor.
scaling factor.