How do I use quiver in Python for polar?

Question

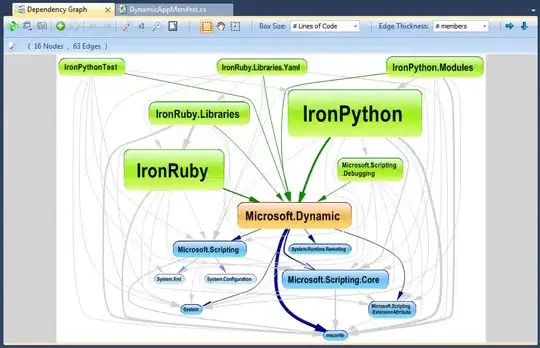
Firstly, yes I have read previous threads and documentation about this issue, for example How to make a quiver plot in polar coordinates. This didn't help me all the way. Let me show you what I am working with and then some code. This is a converging canal, it shows a velocity/vector field. Clearly I only have a radial component, but it changes with the angle theta. This pattern of arrows repeats itself as we go down(stream) towards alpha. So it should be simple to plot, right. Here is the equation for the radial velocity component:

Now, before I show my code, I have stored values of f(theta) for a number of thetas. This function, f, has to be numerically solved and I have stored it as a vector, u[0]. This what I do in my code as of now:

radii = np.linspace(0.1,1,11)
thetas = np.linspace(-alpha,alpha,20)
theta, r = np.meshgrid(thetas, radii)

q = 0.0001


dr = [-q/x for x in radii]*u_sol[0]
dt = 0

f = plt.figure()
ax = f.add_subplot(111, polar=True)

ax.quiver(theta, r, dr * cos(theta) - dt * sin (theta), dr * sin(theta) +     
dt* cos(theta))

The fifth expression for the variable dr was a desperate attempt at multiplying all r of a fix length in the meshgrid with u[0], but these do not have the same dimensions, therefore it doesn't work. So I am stuck.

My question is how I obtain a vectorfield for the converging canal? I can't really put the last pieces togetether, do I manipulate the meshgrid?

Results so far in MATLAB:

Edit The code above was taken from the link in the beginning of my text. I made some changes to dr and dt, but otherwise nothing.

Answer 1

The only real problem with your code was a numpy problem, i.e. in your dr has the wrong dimensions. With slight adjustments to your code:

from matplotlib import pyplot as plt
import numpy as np

#to make the code runnable
u_sol = [1]
alpha0 = 5*np.pi/180
alpha = 10*np.pi/180

radii = np.linspace(0.2,1,10)
print(radii)
thetas = np.linspace(alpha0-alpha,alpha0+alpha,20)
print(thetas)
theta, r = np.meshgrid(thetas, radii)

q = 0.0001


#dr = [-q/x for x in radii]*u_sol[0]
dr = -q/r
dt = 0

f = plt.figure()
ax = f.add_subplot(111, polar=True)

ax.quiver(
    theta, r,
    dr * np.cos(theta) - dt * np.sin(theta),
    dr * np.sin(theta) + dt * np.cos(theta),
)

plt.show()

I get the following image:

Note that in the radii definition, I moved the lower limit from 0.1 to 0.2 as otherwise the arrows get so long that they point to the other side of the origin, which looks quite weird.