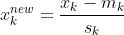Cost function in logistic regression gives NaN as a result

Question

I am implementing logistic regression using batch gradient descent. There are two classes into which the input samples are to be classified. The classes are 1 and 0. While training the data, I am using the following sigmoid function:

t = 1 ./ (1 + exp(-z));

where

z = x*theta

And I am using the following cost function to calculate cost, to determine when to stop training.

function cost = computeCost(x, y, theta)
    htheta = sigmoid(x*theta);
    cost = sum(-y .* log(htheta) - (1-y) .* log(1-htheta));
end

I am getting the cost at each step to be NaN as the values of htheta are either 1 or zero in most cases. What should I do to determine the cost value at each iteration?

This is the gradient descent code for logistic regression:

function [theta,cost_history] = batchGD(x,y,theta,alpha)

cost_history = zeros(1000,1);

for iter=1:1000
  htheta = sigmoid(x*theta);
  new_theta = zeros(size(theta,1),1);
  for feature=1:size(theta,1)
    new_theta(feature) = theta(feature) - alpha * sum((htheta - y) .*x(:,feature))                         
  end
  theta = new_theta;
  cost_history(iter) = computeCost(x,y,theta);
end
end

Answer 1

There are two possible reasons why this may be happening to you.

The data is not normalized

This is because when you apply the sigmoid / logit function to your hypothesis, the output probabilities are almost all approximately 0s or all 1s and with your cost function, log(1 - 1) or log(0) will produce -Inf. The accumulation of all of these individual terms in your cost function will eventually lead to NaN.

Specifically, if y = 0 for a training example and if the output of your hypothesis is log(x) where x is a very small number which is close to 0, examining the first part of the cost function would give us 0*log(x) and will in fact produce NaN. Similarly, if y = 1 for a training example and if the output of your hypothesis is also log(x) where x is a very small number, this again would give us 0*log(x) and will produce NaN. Simply put, the output of your hypothesis is either very close to 0 or very close to 1.

This is most likely due to the fact that the dynamic range of each feature is widely different and so a part of your hypothesis, specifically the weighted sum of x*theta for each training example you have will give you either very large negative or positive values, and if you apply the sigmoid function to these values, you'll get very close to 0 or 1.

One way to combat this is to normalize the data in your matrix before performing training using gradient descent. A typical approach is to normalize with zero-mean and unit variance. Given an input feature x_k where k = 1, 2, ... n where you have n features, the new normalized feature x_k^{new} can be found by:

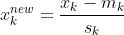
m_k is the mean of the feature k and s_k is the standard deviation of the feature k. This is also known as standardizing data. You can read up on more details about this on another answer I gave here: How does this code for standardizing data work?

Because you are using the linear algebra approach to gradient descent, I'm assuming you have prepended your data matrix with a column of all ones. Knowing this, we can normalize your data like so:

mX = mean(x,1); 
mX(1) = 0; 
sX = std(x,[],1); 
sX(1) = 1; 
xnew = bsxfun(@rdivide, bsxfun(@minus, x, mX), sX);

The mean and standard deviations of each feature are stored in mX and sX respectively. You can learn how this code works by reading the post I linked to you above. I won't repeat that stuff here because that isn't the scope of this post. To ensure proper normalization, I've made the mean and standard deviation of the first column to be 0 and 1 respectively. xnew contains the new normalized data matrix. Use xnew with your gradient descent algorithm instead. Now once you find the parameters, to perform any predictions you must normalize any new test instances with the mean and standard deviation from the training set. Because the parameters learned are with respect to the statistics of the training set, you must also apply the same transformations to any test data you want to submit to the prediction model.

Assuming you have new data points stored in a matrix called xx, you would do normalize then perform the predictions:

xxnew = bsxfun(@rdivide, bsxfun(@minus, xx, mX), sX);

Now that you have this, you can perform your predictions:

pred = sigmoid(xxnew*theta) >= 0.5;

You can change the threshold of 0.5 to be whatever you believe is best that determines whether examples belong in the positive or negative class.

The learning rate is too large

As you mentioned in the comments, once you normalize the data the costs appear to be finite but then suddenly go to NaN after a few iterations. Normalization can only get you so far. If your learning rate or alpha is too large, each iteration will overshoot in the direction towards the minimum and would thus make the cost at each iteration oscillate or even diverge which is what is appearing to be happening. In your case, the cost is diverging or increasing at each iteration to the point where it is so large that it can't be represented using floating point precision.

As such, one other option is to decrease your learning rate alpha until you see that the cost function is decreasing at each iteration. A popular method to determine what the best learning rate would be is to perform gradient descent on a range of logarithmically spaced values of alpha and seeing what the final cost function value is and choosing the learning rate that resulted in the smallest cost.

---

Using the two facts above together should allow gradient descent to converge quite nicely, assuming that the cost function is convex. In this case for logistic regression, it most certainly is.

Answer 2

Let's assume you have an observation where:

• the true value is y_i = 1
• your model is quite extreme and says that P(y_i = 1) = 1

Then your cost function will get a value of NaN because you're adding 0 * log(0), which is undefined. Hence:

Your formula for the cost function has a problem (there is a subtle 0, infinity issue)!

As @rayryeng pointed out, 0 * log(0) produces a NaN because 0 * Inf isn't kosher. This is actually a huge problem: if your algorithm believes it can predict a value perfectly, it incorrectly assigns a cost of NaN.

Instead of:

cost = sum(-y .* log(htheta) - (1-y) .* log(1-htheta));

You can avoid multiplying 0 by infinity by instead writing your cost function in Matlab as:

y_logical = y == 1;
cost = sum(-log(htheta(y_logical))) + sum( - log(1 - htheta(~y_logical)));

The idea is if y_i is 1, we add -log(htheta_i) to the cost, but if y_i is 0, we add -log(1 - htheta_i) to the cost. This is mathematically equivalent to -y_i * log(htheta_i) - (1 - y_i) * log(1- htheta_i) but without running into numerical problems that essentially stem from htheta_i being equal to 0 or 1 within the limits of double precision floating point.

Answer 3

It happened to me because an indetermination of the type:

0*log(0)

This can happen when one of the predicted values Y equals either 0 or 1. In my case the solution was to add an if statement to the python code as follows:

y * np.log (Y)  + (1-y) * np.log (1-Y) if ( Y != 1 and Y != 0 ) else 0

This way, when the actual value (y) and the predicted one (Y) are equal, no cost needs to be computed, which is the expected behavior.

(Notice that when a given Y is converging to 0 the left addend is canceled (because of y=0) and the right addend tends toward 0. The same happens when Y converges to 1, but with the opposite addend.)

(There is also a very rare scenario, which you probably won't need to worry about, where y=0 and Y=1 or viceversa, but if your dataset is standarized and the weights are properly initialized it won't be an issue.)