opencv euclidean clustering vs findContours

Question

I have the following image mask:

I want to apply something similar to cv::findContours, but that algorithm only joins connected points in the same groups. I want to do this with some tolerance, i.e., I want to add the pixels near each other within a given radius tolerance: this is similar to Euclidean distance hierarchical clustering.

Is this implemented in OpenCV? Or is there any fast approach for implementing this?

What I want is something similar to this,

http://www.pointclouds.org/documentation/tutorials/cluster_extraction.php

applied to the white pixels of this mask.

Thank you.

Answer 1

You can use partition for this:

partition splits an element set into equivalency classes. You can define your equivalence class as all points within a given euclidean distance (radius tolerance)

If you have C++11, you can simply use a lambda function:

int th_distance = 18; // radius tolerance

int th2 = th_distance * th_distance; // squared radius tolerance
vector<int> labels;

int n_labels = partition(pts, labels, [th2](const Point& lhs, const Point& rhs) {
    return ((lhs.x - rhs.x)*(lhs.x - rhs.x) + (lhs.y - rhs.y)*(lhs.y - rhs.y)) < th2; 
});

otherwise, you can just build a functor (see details in the code below).

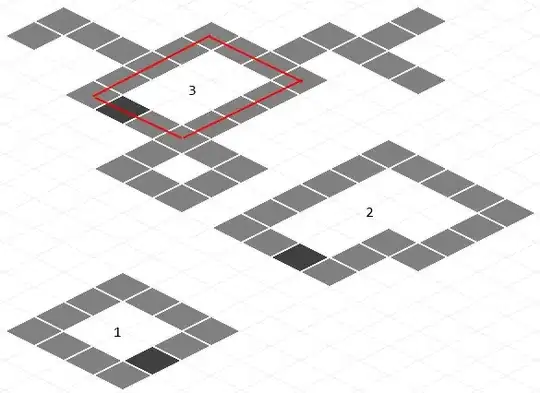
With appropriate radius distance (I found 18 works good on this image), I got:

Full code:

#include <opencv2\opencv.hpp>
#include <vector>
#include <algorithm>

using namespace std;
using namespace cv;

struct EuclideanDistanceFunctor
{
    int _dist2;
    EuclideanDistanceFunctor(int dist) : _dist2(dist*dist) {}

    bool operator()(const Point& lhs, const Point& rhs) const
    {
        return ((lhs.x - rhs.x)*(lhs.x - rhs.x) + (lhs.y - rhs.y)*(lhs.y - rhs.y)) < _dist2;
    }
};

int main()
{
    // Load the image (grayscale)
    Mat1b img = imread("path_to_image", IMREAD_GRAYSCALE);

    // Get all non black points
    vector<Point> pts;
    findNonZero(img, pts);

    // Define the radius tolerance
    int th_distance = 18; // radius tolerance

    // Apply partition 
    // All pixels within the radius tolerance distance will belong to the same class (same label)
    vector<int> labels;

    // With functor
    //int n_labels = partition(pts, labels, EuclideanDistanceFunctor(th_distance));

    // With lambda function (require C++11)
    int th2 = th_distance * th_distance;
    int n_labels = partition(pts, labels, [th2](const Point& lhs, const Point& rhs) {
        return ((lhs.x - rhs.x)*(lhs.x - rhs.x) + (lhs.y - rhs.y)*(lhs.y - rhs.y)) < th2;
    });

    // You can save all points in the same class in a vector (one for each class), just like findContours
    vector<vector<Point>> contours(n_labels);
    for (int i = 0; i < pts.size(); ++i)
    {
        contours[labels[i]].push_back(pts[i]);
    }

    // Draw results

    // Build a vector of random color, one for each class (label)
    vector<Vec3b> colors;
    for (int i = 0; i < n_labels; ++i)
    {
        colors.push_back(Vec3b(rand() & 255, rand() & 255, rand() & 255));
    }

    // Draw the labels
    Mat3b lbl(img.rows, img.cols, Vec3b(0, 0, 0));
    for (int i = 0; i < pts.size(); ++i)
    {
        lbl(pts[i]) = colors[labels[i]];
    }

    imshow("Labels", lbl);
    waitKey();

    return 0;
}

Answer 2

I suggest to use DBSCAN algorithm. It is exactly what you are looking for. Use a simple Euclidean Distance or even Manhattan Distance may work better. The input is all white points(threshold-ed). The output is a groups of points(your connected component)

Here is a DBSCAN C++ implenetation

EDIT: I tried DBSCAN my self and here is the result:

As you see, Just the really connected points are considered as one cluster.

This result was obtained using the standerad DBSCAN algorithm with EPS=3 (static no need to be tuned) MinPoints=1 (static also) and Manhattan Distance