Find all peaks for Mat() in OpenCV C++

Question

I want to find all maximums (numbers of non-zero pixels) for my image. I need it to divide my picture such way:

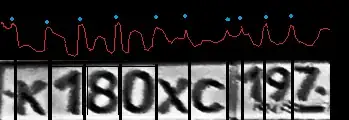
So, i already asked question, how to project all image to one of the axis, and now i need to find all maximums on this one-row image. Here's my part of the code:

void segment_plate (Mat input_image) {
    double minVal; 
    double maxVal; 
    Point minLoc; 
    Point maxLoc;
    Mat work_image = input_image;
    Mat output;
    //binarize image
    adaptiveThreshold(work_image,work_image, 255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 15, 10);  
    //project it to one axis
    reduce(work_image,output,0,CV_REDUCE_SUM,CV_32S);

    //find minimum and maximum falue for ALL image
    minMaxLoc(output, &minVal,&maxVal,&minLoc,&maxLoc);
    cout << "min val : " << minVal << endl;
    cout << "max val: " << maxVal << endl;

As you can see, i could find one maximum and one minimum for all picture, but i need to find local maximums. Thanks for any help!

EDIT Ok, so i made a mistake, i need to find peaks for this vector. I've used this code to find first peak:

int findPeakUtil(Mat arr, int low, int high, int n) {
// Find index of middle element
    int mid = low + (high - low)/2;  /* (low + high)/2 */

// Compare middle element with its neighbours (if neighbours exist)
    if ((mid == 0 || arr.at<int>(0,mid-1) <= arr.at<int>(0,mid)) &&
        (mid == n-1 || arr.at<int>(0,mid+1) <= arr.at<int>(0,mid)))
    return mid;

// If middle element is not peak and its left neighbor is greater than it
// then left half must have a peak element
    else if (mid > 0 && arr.at<int>(0,mid-1) > arr.at<int>(0,mid))
    return findPeakUtil(arr, low, (mid - 1), n);

// If middle element is not peak and its right neighbor is greater than it
// then right half must have a peak element
    else return findPeakUtil(arr, (mid + 1), high, n);
}

// A wrapper over recursive function findPeakUtil()
int findPeak(Mat arr, int n) {
   return findPeakUtil(arr, 0, n-1, n);
}

So now my code looks like:

void segment_plate (Mat input_image) {
    Mat work_image = input_image;
    Mat output;
    //binarize image
    adaptiveThreshold(work_image,work_image, 255, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 15, 10);  
    //project it to one axis
    reduce(work_image,output,0,CV_REDUCE_SUM,CV_32S);
    int n = output.cols;
    printf("Index of a peak point is %d", findPeak(output, n));

But how can i find another peaks? The algorithm of peak finding i took from here.

Answer 1

One way I can think about to find peaks is to find the first derivative and then find the negative numbers of it.

for example,

a = [ 1, 2, 3, 4, 4, 5, 6, 3, 4]

in this example the peak is 6 in the position 6 and 4 in the las position. so, if you extend the vector (0 at the end) and apply the first derivative (a[i] - a[i-1]) you'll get

a_deriv = [1,1,1,0,1,1,-3,1,-4]

where the negative numbers are in the position of the peaks. In this case, -3 is in position 6 and -4 in position 8, that is where the peaks are located.

This is a way to do it.... but is not the only one.

Note that this method will count only the last number in a plateau as the peak ( you can find a plateau when two numbers share the peak because they have the same value and are consecutive)

Hope this helps you