gradient descent seems to fail

Question

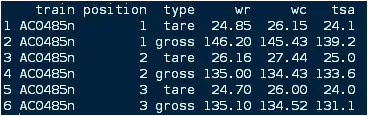
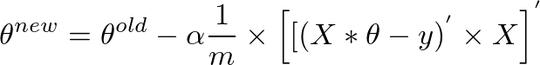I implemented a gradient descent algorithm to minimize a cost function in order to gain a hypothesis for determining whether an image has a good quality. I did that in Octave. The idea is somehow based on the algorithm from the machine learning class by Andrew Ng

Therefore I have 880 values "y" that contains values from 0.5 to ~12. And I have 880 values from 50 to 300 in "X" that should predict the image's quality.

Sadly the algorithm seems to fail, after some iterations the value for theta is so small, that theta0 and theta1 become "NaN". And my linear regression curve has strange values...

here is the code for the gradient descent algorithm: (theta = zeros(2, 1);, alpha= 0.01, iterations=1500)

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)

m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters


    tmp_j1=0;
for i=1:m, 
    tmp_j1 = tmp_j1+ ((theta (1,1) + theta (2,1)*X(i,2)) - y(i));
end

    tmp_j2=0;
for i=1:m, 
    tmp_j2 = tmp_j2+ (((theta (1,1) + theta (2,1)*X(i,2)) - y(i)) *X(i,2)); 
end

    tmp1= theta(1,1) - (alpha *  ((1/m) * tmp_j1))  
    tmp2= theta(2,1) - (alpha *  ((1/m) * tmp_j2))  

    theta(1,1)=tmp1
    theta(2,1)=tmp2

    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);
end
end

And here is the computation for the costfunction:

function J = computeCost(X, y, theta)   %

m = length(y); % number of training examples
J = 0;
tmp=0;
for i=1:m, 
    tmp = tmp+ (theta (1,1) + theta (2,1)*X(i,2) - y(i))^2; %differenzberechnung
end
J= (1/(2*m)) * tmp
end

i guess u skipped vectorisation lecture - same as me ;) https://class.coursera.org/ml-007/lecture/30 — HaveAGuess, Oct 19 '14 at 23:57

jerrymouse · Answer 1 · 2017-03-23T10:22:12.727

If you are wondering how the seemingly complex looking for loop can be vectorized and cramped into a single one line expression, then please read on. The vectorized form is:

theta = theta - (alpha/m) * (X' * (X * theta - y))

Given below is a detailed explanation for how we arrive at this vectorized expression using gradient descent algorithm:

This is the gradient descent algorithm to fine tune the value of θ:

Assume that the following values of X, y and θ are given:

m = number of training examples
n = number of features + 1

Here

m = 5 (training examples)
n = 4 (features+1)
X = m x n matrix
y = m x 1 vector matrix
θ = n x 1 vector matrix
xⁱ is the i^th training example
x_j is the j^th feature in a given training example

Further,

h(x) = ([X] * [θ]) (m x 1 matrix of predicted values for our training set)
h(x)-y = ([X] * [θ] - [y]) (m x 1 matrix of Errors in our predictions)

whole objective of machine learning is to minimize Errors in predictions. Based on the above corollary, our Errors matrix is m x 1 vector matrix as follows:

To calculate new value of θ_j, we have to get a summation of all errors (m rows) multiplied by j^th feature value of the training set X. That is, take all the values in E, individually multiply them with j^th feature of the corresponding training example, and add them all together. This will help us in getting the new (and hopefully better) value of θ_j. Repeat this process for all j or the number of features. In matrix form, this can be written as:

This can be simplified as:

[E]' x [X] will give us a row vector matrix, since E' is 1 x m matrix and X is m x n matrix. But we are interested in getting a column matrix, hence we transpose the resultant matrix.

More succinctly, it can be written as:

Since (A * B)' = (B' * A'), and A'' = A, we can also write the above as

This is the original expression we started out with:

theta = theta - (alpha/m) * (X' * (X * theta - y))

This was tremendously helpful - the verbosity of the matrix math made all the difference for me. — rbellamy, Jun 22 '19 at 22:06

score 31 · Answer 2 · answered Apr 28 '13 at 18:50

31

i vectorized the theta thing... may could help somebody

theta = theta - (alpha/m *  (X * theta-y)' * X)';

answered Apr 28 '13 at 18:50

Markus

1,465
4
18
29

7

This one is the right answer. Another way to write this: `theta = theta - alpha / m * (X' * (X * theta - y));` It's better to use vectoriaztion when possible. – Xiao Hanyu Mar 31 '14 at 12:52
ah excellent, i knew there had to be a way but I couldnt get the math right on paper ;) – HaveAGuess Oct 20 '14 at 00:12
For those copy-and-pasting: this is the correct update only for a *linear* activation function, not for sigmoids and all the other stuff. – davidhigh May 14 '16 at 11:50
Why isn't it like this: `theta = theta - (alpha/m) * sum(((X * theta) - y)' * X);`? The gradient descent equation contains a summation. – SalmaFG May 14 '16 at 17:12
1

you only want to sum accross the values for each theta not all the theta results. X' * (x * theta -y) needs to end up with a 1X2 vector. Using the sum function would result in a 1X1 vector which would ruin the matrix algebra. – user249806 May 25 '16 at 15:47
Written a detailed answer below to explain why Markus' answer is correct http://stackoverflow.com/a/42330833/842837 – jerrymouse Feb 19 '17 at 18:03

Thomas Jungblut · Accepted Answer · 2013-10-16T05:54:21.223

25

I think that your computeCost function is wrong. I attended NG's class last year and I have the following implementation (vectorized):

m = length(y);
J = 0;
predictions = X * theta;
sqrErrors = (predictions-y).^2;

J = 1/(2*m) * sum(sqrErrors);

The rest of the implementation seems fine to me, although you could also vectorize them.

theta_1 = theta(1) - alpha * (1/m) * sum((X*theta-y).*X(:,1));
theta_2 = theta(2) - alpha * (1/m) * sum((X*theta-y).*X(:,2));

Afterwards you are setting the temporary thetas (here called theta_1 and theta_2) correctly back to the "real" theta.

Generally it is more useful to vectorize instead of loops, it is less annoying to read and to debug.

edited Oct 16 '13 at 05:54

answered May 07 '12 at 17:32

Thomas Jungblut

20,854
6
68
91

thanks ;) (I attended the course last year too and wanted to map the solution on a current problem;), so your answer should be okay ;)) – Tyzak May 08 '12 at 18:15
BTW, maybe I am forgetting but should 1st one not be ? theta_1 = theta(1) - alpha * (1/m) * sum(X*theta - y) – Sumit Nigam Nov 06 '13 at 15:05
Thanks, I used a loop instead of vectorisation and had same problem, what a life saver! Agreed looks smarter – HaveAGuess Oct 19 '14 at 23:18
and vectorized form is also scalable across multiple features – Edwin O. May 18 '18 at 09:04

score 2 · Answer 4 · edited Mar 16 '14 at 10:57

2

If you are OK with using a least-squares cost function, then you could try using the normal equation instead of gradient descent. It's much simpler -- only one line -- and computationally faster.

Here is the normal equation: http://mathworld.wolfram.com/NormalEquation.html

And in octave form:

theta = (pinv(X' * X )) * X' * y

Here is a tutorial that explains how to use the normal equation: http://www.lauradhamilton.com/tutorial-linear-regression-with-octave

edited Mar 16 '14 at 10:57

Stefan Gehrig

82,642
24
155
189

answered Jul 29 '13 at 14:53

user2437742

93
2
6

The question is about Gradient descent. Normal equation can also be used. – naren Mar 06 '16 at 16:03

score 2 · Answer 5 · answered Mar 02 '15 at 07:29

While not scalable like a vectorized version, a loop-based computation of a gradient descent should generate the same results. In the example above, the most probably case of the gradient descent failing to compute the correct theta is the value of alpha.

With a verified set of cost and gradient descent functions and a set of data similar with the one described in the question, theta ends up with NaN values just after a few iterations if alpha = 0.01. However, when set as alpha = 0.000001, the gradient descent works as expected, even after 100 iterations.

score 0 · Answer 6 · answered Aug 16 '16 at 12:43

Using only vectors here is the compact implementation of LR with Gradient Descent in Mathematica:

Theta = {0, 0}
alpha = 0.0001;
iteration = 1500;
Jhist = Table[0, {i, iteration}];
Table[  
  Theta = Theta - 
  alpha * Dot[Transpose[X], (Dot[X, Theta] - Y)]/m; 
  Jhist[[k]] = 
  Total[ (Dot[X, Theta] - Y[[All]])^2]/(2*m); Theta, {k, iteration}]

Note: Of course one assumes that X is a n * 2 matrix, with X[[,1]] containing only 1s'

score 0 · Answer 7 · answered Nov 13 '17 at 14:06

0

This should work:-

theta(1,1) = theta(1,1) - (alpha*(1/m))*((X*theta - y)'* X(:,1) ); 

theta(2,1) = theta(2,1) - (alpha*(1/m))*((X*theta - y)'* X(:,2) );

answered Nov 13 '17 at 14:06

Gator-aid

51
4

score 0 · Answer 8 · answered May 18 '18 at 09:06

0

its cleaner this way, and vectorized also

predictions = X * theta;
errorsVector = predictions - y;
theta = theta - (alpha/m) * (X' * errorsVector);

answered May 18 '18 at 09:06

Edwin O.

4,998
41
44

score 0 · Answer 9 · answered Oct 12 '18 at 16:46

If you remember the first Pdf file for Gradient Descent form machine Learning course, you would take care of learning rate. Here is the note from the mentioned pdf.

Implementation Note: If your learning rate is too large, J(theta) can di- verge and blow up', resulting in values which are too large for computer calculations. In these situations, Octave/MATLAB will tend to return NaNs. NaN stands fornot a number' and is often caused by undened operations that involve - infinity and +infinity.

gradient descent seems to fail

9 Answers9

Linked