Gradient Descent in Matlab

Question

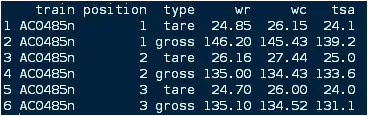
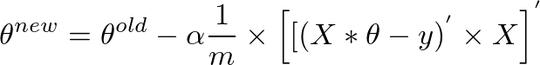I am taking machine learning class in courseera. The machine learning is a pretty area for me. In first programming exercise I am having some difficulties in gradient decent algorithm. If anyone can help me I will be appreciate.

Here is the instructions for updating thetas;

"You will implement gradient descent in the file gradientDescent.m. The loop structure has been written for you, and you only need to supply the updates to θ within each iteration.

    function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
    %GRADIENTDESCENT Performs gradient descent to learn theta
    %   theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by 
    %   taking num_iters gradient steps with learning rate alpha

   % Initialize some useful values
   m = length(y); % number of training examples
   J_history = zeros(num_iters, 1);

   for iter = 1:num_iters

% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
%               theta. 
%
% Hint: While debugging, it can be useful to print out the values
%       of the cost function (computeCost) and gradient here.
%
    % ============================================================

% Save the cost J in every iteration    
J_history(iter) = computeCost(X, y, theta);

end

end

So here is what I did to update thetas simultaneously;

    temp0 = theta(1,1) - (alpha/m)*sum((X*theta-y));
    temp1 = theta(2,1) - (alpha/m)*sum((X*theta-y).*X);
    theta(1,1) = temp0;
    theta(2,1) = temp1;

I am getting error when I run this code. Can anyone help me please?

Answer 1

I have explained why you can use the vectorized form:

theta = theta - (alpha/m) * (X' * (X * theta - y)); or the equivalent

theta = theta - (alpha/m) * ((X * theta - y)' * X)';

in this answer.

Quoting it below:

---

Explanation for the matrix version of gradient descent algorithm:

This is the gradient descent algorithm to fine tune the value of θ:

Assume that the following values of X, y and θ are given:

• m = number of training examples
• n = number of features + 1

Here

• m = 5 (training examples)
• n = 4 (features+1)
• X = m x n matrix
• y = m x 1 vector matrix
• θ = n x 1 vector matrix
• xⁱ is the i^th training example
• x_j is the j^th feature in a given training example

Further,

• h(x) = ([X] * [θ]) (m x 1 matrix of predicted values for our training set)
• h(x)-y = ([X] * [θ] - [y]) (m x 1 matrix of Errors in our predictions)

whole objective of machine learning is to minimize Errors in predictions. Based on the above corollary, our Errors matrix is m x 1 vector matrix as follows:

To calculate new value of θ_j, we have to get a summation of all errors (m rows) multiplied by j^th feature value of the training set X. That is, take all the values in E, individually multiply them with j^th feature of the corresponding training example, and add them all together. This will help us in getting the new (and hopefully better) value of θ_j. Repeat this process for all j or the number of features. In matrix form, this can be written as:

This can be simplified as:

• [E]' x [X] will give us a row vector matrix, since E' is 1 x m matrix and X is m x n matrix. But we are interested in getting a column matrix, hence we transpose the resultant matrix.

More succinctly, it can be written as:

The same result can also be written as:

Answer 2

theta = theta - (alpha/m) * (X' * (X * theta - y));

this is the right answer

Answer 3

The error that you got Error using .* Matrix dimensions must agree. Error in gradientDescent (line 20) temp1 = theta(2,1) - (alpha/m)*sum((X*theta-y).*X); means that the .* is not working. So, before that line, add in the following code:

size(X*theta-y)
size(X)

If you want to do (X*theta-y).*X, then both X*theta-y and X should be the same size. If they aren't, you will need to check your algorithm.

Answer 4

temp0 = theta(1,1) - (alpha/m)*sum((X*theta-y));
temp1 = theta(2,1) - (alpha/m)*sum((X*theta-y).*X(:,2));
theta(1,1) = temp0;
theta(2,1) = temp1;

Or you can use the code below. It's simpler. There are only two parameters theta1 and theta2. But if more parameters exist, it's much better.

for i=1:2
    theta(i) = theta(i) - (alpha/m)*sum((X*theta-y).*X(:,i));
end

Answer 5

There is one thing to note in this question:

X = [ones(m, 1), data(:,1)]; 

so

theta = theta - (alpha / m) * (X' * (X * theta - y));

and

temp0 = theta(1, 1) - (alpha / m) * sum((X * theta - y));
temp1 = theta(2, 1) - (alpha / m) * sum((X * theta - y) .* X(:, 2));
theta(1, 1) = temp0;
theta(2, 1) = temp1;

both are right