Java: Finding the Outermost Vertices of a Convex Polygon

Question

Original post:

I'm trying to find the outermost vertices of a convex polygon (with relation to a point P outside the polygon). For now, I'm only concerned with rectangles (however, I'd like an algorithm that works with any convex polygon).

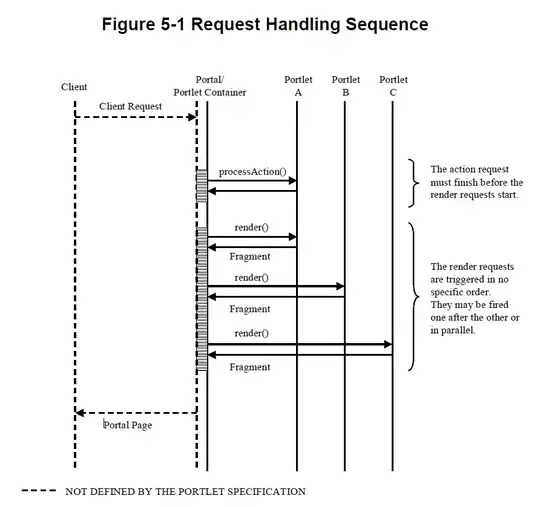
Point Demonstration

My plan is to construct a line from external point P to central point C. From this line of reference, I will construct lines from point P to points 1, 2, 3 and 4. Since points 2 and 4 will have the largest (most positive) and smallest (most negative) angles from the line of reference, they will be identified as the outermost vertices.

Is this the best algorithm for the job? How does one calculate angles from a reference angle (preferably in Java)?

Update for clarification:

enter image description here

I've drawn the lines (line of reference in red). As you can see, the line from P to 2 creates the largest angle on one side of the line of reference, while the line from P to 4 creates the largest angle of the other side. Hence, these are the outermost vertices.

well, angle between two points A and B should be atan2(b.y,b.x) - atan2(a.y,a.x) — HugoRune, Apr 01 '12 at 21:16
But simply taking the largest and second-largest angle might not solve the problem for all cases... I think. — Peter, Apr 01 '12 at 21:19
Why not just consider farthest points from the line you draw from P to C? — m0skit0, Apr 01 '12 at 21:40
"I'm trying to find the outermost vertices of a convex polygon (with relation to a point P outside the polygon)." - I don't understand. Can you point to a reference? — emory, Apr 01 '12 at 22:05
No, not really. I still don't know what you mean by "outermost." — Louis Wasserman, Apr 01 '12 at 22:18
@Peter actually the picture is not helpful to me. When I look at the picture, I think vertex 3, but the commentary suggests the answer is vertices 2 and 4. The concept is not clear to me. — emory, Apr 01 '12 at 22:31

score 2 · Answer 1 · answered Apr 02 '12 at 01:50

2

This is pretty much the convex hull problem. You would be looking for a set of vertices (x₁, x₂) around a polygon. The methodology that would be applied is called "quick-hull", analogous to quicksort (in that we divide our region of points every time we step through). It is also a safe assumption that P can be used as a mid-point between an arbitrary starting point and its parallel ending point, so you would get a convex hull around P.

It would take a while to produce some reliable Java to poke at (from my happenstance), but I think that the Wikipedia entry will give you a great starting point.

answered Apr 02 '12 at 01:50

Makoto

104,088
27
192
230

I'm sorry... I don't think this is very similar to the convex hull problem. The boundaries of the shape are known, and I'm not using any Minkowski sums. Additionally, **P** *is* the starting point for the calculations. I'm looking for the *outermost vertices* with relation to external point **P**. Therefore, the operation is iterative and requires no step-wise division. – Peter Apr 02 '12 at 19:07
2

The convex hull of the points 1,2,3,4 is known. The convex hull of the points P,1,2,3,4 is not known. I think the outermost points are the two points adjacent to P in the convex hull of P,1,2,3,4. Notice 1 is not part of the convex hull of P,1,2,3,4. – emory Apr 02 '12 at 19:52
Ah. I understand now. So is a convex hull algorithm the quickest way to solve this? – Peter Apr 02 '12 at 20:35
1

@Peter: It would be a very quick way to solve it, yes; Quick-hull can achieve O(N*lg(N)) performance on average, with a worst-case of O(n^2) (highly unlikely). – Makoto Apr 02 '12 at 20:48

Peter · Accepted Answer · 2013-11-22T00:51:03.843

I solved the problem as follows:

            // code simplified for demonstration
            double angleBetweenVertices;
            double maxAngleBetweenVertices;
            vectorA.setStartingPoint(outerPoint);
            vectorA.setTerminationPoint(polygonCenter);
            vectorB.setStartingPoint(outerPount);

            // For each vertex, calculate the angle between the outer point, the polygon's center and the vertex
            for (Point2D.Double vertex : vertices) {    
                vectorB.setTerminationPoint(vertex);
                double angleBetweenVertices = 
                    Math.toDegrees(
                        Math.atan2(
                            (vectorA.perpDotProduct(vectorB)),
                            (vectorA.dotProduct(vectorB)) 
                        )
                    );

                // Update the min and Max
                if (angleBetweenVertices >= maxAngleBetweenVertices) {
                    maxVertex = vertex;
                    maxAngleBetweenVertices = angleBetweenVertices;
                } else if (angleBetweenVertices <= minAngleBetweenVertices) {
                    minVertex = vertex;
                    minAngleBetweenVertices = angleBetweenVertices;
                }
            }

Gangnus · Answer 3 · 2012-05-18T15:18:30.983

0

The use of trigonometry is extremely slow. You should use another angle comparison.

For an angle between two flat vectors:

cos(OA, OB) = (OA_x * OB_x + OA_y* OB_y) / sqrt((OA_x² + OA_y²)* (OB_x ² + OB_y²))

I think, you can compare angles having cosines.

edited May 18 '12 at 15:18

answered Apr 01 '12 at 21:13

Gangnus

24,044
16
90
149

Java: Finding the Outermost Vertices of a Convex Polygon

Original post:

Update for clarification:

3 Answers3