9

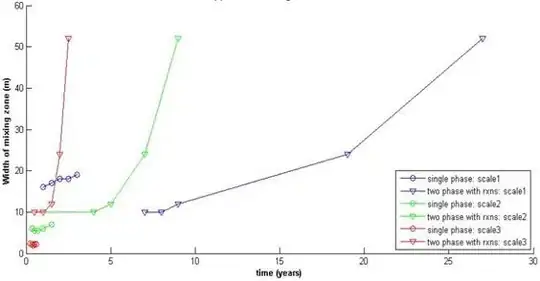
I have various plots (with hold on) as show in the following figure: enter image description here

I would like to know how to find equations of these six curves in Matlab. Thanks.

  • There are any number of equations that would fit those curves. Do you know anything about the underlying relationship? e.g. is it likely to be exponential, quadratic, etc.? – Oliver Charlesworth Mar 30 '12 at 19:50
  • Not clear to me...Are you generating curve from the data yourself or you just have the graph saved as .fig ( I guess that is MATLAB format)? – Jack_of_All_Trades Mar 30 '12 at 19:51
  • @ Oli: I do not know the underlying relationship. @ Jack_of_All_Trades: I am generating curve from the data myself. –  Mar 30 '12 at 19:59
  • @S_H: That's a problem, then. If you don't know the underlying form for the equation, then you will find an infinite number of different equations that fit the data. – Oliver Charlesworth Mar 30 '12 at 20:00

5 Answers5

3

I found interactive fitting tool in Matlab simple and helpful, though somewhat limited in scope:

enter image description here

0

The graph above seems to be linear interpolation. Given vectors X and Y of data, where X contains the arguments and Y the function points, you could do 

f = interp1(X, Y, x)

to get the linearly interpolated value f(x). For example if the data is 

X = [0 1 2 3  4  5];
Y = [0 1 4 9 16 25];

then 

y = interp1(X, Y, 1.5)

should give you a very rough approximation to 1.5^2. interp1 will match the graph exactly, but you might be interested in fancier curve-fitting operations, like spline approximations etc.

richard
  • 605
  • 5
  • 8
  • @richard: I have data which I have plotted and shown in the question. I want to find out the equation of that plot which I do not know. –  Mar 30 '12 at 20:04
  • @S_H just be to be clear, you actually have the numerical data that generated that plot? The equation of the plot, like I said, is linear (http://en.wikipedia.org/wiki/Linear_interpolation); in other words "connect the dots". But this is one of many possible ways to to turn the discrete data into a "curve". You have to be more specific about what you are looking for. – richard Mar 30 '12 at 23:59
  • I think you can see that the plot looks like a curve (than a straight line), and I want to be able to find the equation of that curve. –  Mar 31 '12 at 02:46
  • The data here is of the form {(x_i, y_i) : i = 1,...,N}, a discrete set of points. That is the function, x_i --> y_i. There is no unique "curve" which describes this data. As Jack_of_All_Trades (@Jack_of_All_Trades) mentioned, there are an infinite number of continuous (and differentiable!) curves that are consistent with the discrete data above. – richard Mar 31 '12 at 04:47
0

The advice, though there might be better answer, from me is: try to see the rate of increase in the curve. For example, cubic is more representative than quadratic if the rate of increase seems fast and find the polynomial and compute the deviation error. For irregular curves, you might try spline fitting. I guess there is also a toolbox in matlab for spline fitting.

Jack_of_All_Trades
  • 10,942
  • 18
  • 58
  • 88
0

Does rxns stand for reactions? In that case, your curves are most likely exponential. An exponential function has the form: y = a*exp(b * x) . In your case, y is the width of mixing zone, and x is the time in years. Now, all you need to do is run exponential regression in Matlab to find the optimal values of parameters a and b, and you'll have your equations.

Diego
  • 18,035
  • 5
  • 62
  • 66
0

There is a way to extract information with the current figure handle (gcf) from you graph.

For example, you can get the series that were plotted in a graph:

% Some figure is created and data are plotted on it
figure;
hold on;
A = [ 1 2 3 4 5 7] % Dummy data
B = A.*A % Some other dummy data
plot(A,B);
plot(A.*3,B-1);

% Those three lines of code will get you series that were plotted on your graph
lh=findall(gcf,'type','line'); % Extract the plotted line from the figure handle
xp=get(lh,'xdata'); % Extract the Xs
yp=get(lh,'ydata'); % Extract the Ys

There must be other informations that you can get from the "findall(gcf,...)" methods.

Mesop
  • 5,187
  • 4
  • 25
  • 42