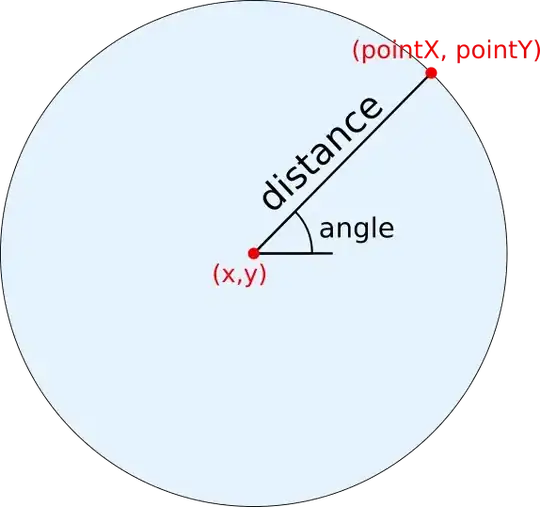
How to get coordinates of a point in a coordinate system when all I have is the origin coordinates (x, y) and the angle from the origin to the point and the distance from the origin to the point?
-
Sounds like more of a math (algebra specifically) question, than a computing question. Do you know the formulae needed to calculate the new point? – Andrew Thompson Mar 26 '12 at 12:04
-
4http://mathworld.wolfram.com/PolarCoordinates.html or http://en.wikipedia.org/wiki/Polar_coordinate_system – Bart Kiers Mar 26 '12 at 12:04
-
Depends on the type of the coordinate system, but most of the time using the simple trigonometric functions called sin(), cos(). – hovanessyan Mar 26 '12 at 12:05
5 Answers
You use Math.cos, Math.sin like this:
pointX = x + distance * Math.cos(angle)
pointY = y + distance * Math.sin(angle)
Note about radians / degrees
Math.cos and Math.sin assumes the argument is given in radians (0…2π). If you have the angle in degrees (0…360), you would use Math.cos(Math.toRadians(angle)) for instance.
- 413,195
- 112
- 811
- 826
-
2+1: Since it actually uses Java-functions, which my answer did not :) – Hannes Ovrén Mar 26 '12 at 12:21
-
If d is the distance and A is the angle, than the coordnates of the point will be
(x+d*Cos(A), y+ d*Sin(A))
- 13,134
- 17
- 77
- 148
-
This is wrong since it does not take into account that the point is offset some other arbitrary point (x,y). – Hannes Ovrén Mar 26 '12 at 12:20
-
@kigurai; Thanks for pointing it. Edited the code. It was in my mind while typing I dont know how I missed it... Anyways thanks once again... – Amit Mar 26 '12 at 12:44
If r is the distance from origin and a is the angle (in radians) between x-axis and the point you can easily calculate the coordinates with a conversion from polar coordinates:
x = r*cos(a)
y = r*sin(a)
(this assumes that origin is placed at (0,0), otherwise you should add the displacement to the final result).
The inverse result is made by computing the modulo of the vector (since a distance + angle make a vector) and the arctangent, which can be calculated by using the atan2 funcion.
r = sqrt(x*2+y*2)
a = atan2(y,x)
- 131,802
- 30
- 241
- 343
px = x + r * cos(phi)
py = y + r * sin(phi)
where [px py] is the point you are searching for, [x y] is the "origin", r is the distance and phi is the angle to the target from the origin.
EDIT: http://en.wikipedia.org/wiki/Polar_coordinate_system This link which was helpfully posted by Bart Kiers could yield some background information.
- 21,229
- 9
- 65
- 75
Short answer
// math equations
pointX = distance * cos(angle) + x
pointY = distance * sin(angle) + y
// java code [angle in radian]
double pointX = distance * Math.cos(Math.toRadians(angle)) + x;
double pointY = distance * Math.sin(Math.toRadians(angle)) + y;
Detailed answer
As per below diagram
// finding pointX let's start by
cos(angle) = (pointX - x) / distance
distance * cos(angle) = (pointX - x)
(pointX - x) = distance * cos(angle)
pointX = distance * cos(angle) + x
// finding pointY let's start by
sin(angle) = (pointY - y) / distance
distance * sin(angle) = (pointY - y)
(pointY - y) = distance * sin(angle)
pointY = distance * sin(angle) + y
- 17,392
- 11
- 61
- 88