6

I would like to know if i can use NetworkX to implement hitting time? Basically I want to calculate the hitting time between any 2 nodes in a graph. My graph is unweighted and undirected. If I understand hitting time correctly, it is very similar to the idea of PageRank.

Any idea how can I implement hitting time using the PageRank method provided by NetworkX?

May I know if there's any good starting point to work with?

I've checked: MapReduce, Python and NetworkX but not quite sure how it works.

Community
  • 1
  • 1
DjangoRocks
  • 13,598
  • 7
  • 37
  • 52

1 Answers1

15

You don't need networkX to solve the problem, numpy can do it if you understand the math behind it. A undirected, unweighted graph can always be represented by a [0,1] adjacency matrix. nth powers of this matrix represent the number of steps from (i,j) after n steps. We can work with a Markov matrix, which is a row normalized form of the adj. matrix. Powers of this matrix represent a random walk over the graph. If the graph is small, you can take powers of the matrix and look at the index (start, end) that you are interested in. Make the final state an absorbing one, once the walk hits the spot it can't escape. At each power n you get probability that you'll have diffused from (i,j). The hitting time can be computed from this function (as you know the exact hit time for discrete steps).

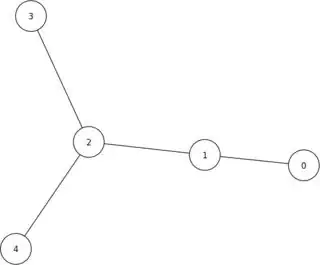
Below is an example with a simple graph defined by the edge list. At the end, I plot this hitting time function. As a reference point, this is the graph used:

enter image description here

from numpy import *

hit_idx = (0,4)

# Define a graph by edge list
edges = [[0,1],[1,2],[2,3],[2,4]]

# Create adj. matrix
A = zeros((5,5))
A[zip(*edges)] = 1
# Undirected condition
A += A.T

# Make the final state an absorbing condition
A[hit_idx[1],:] = 0
A[hit_idx[1],hit_idx[1]] = 1

# Make a proper Markov matrix by row normalizing
A = (A.T/A.sum(axis=1)).T

B = A.copy()
Z = []
for n in xrange(100):
    Z.append( B[hit_idx] )
    B = dot(B,A)

from pylab import *
plot(Z)
xlabel("steps")
ylabel("hit probability")
show()

enter image description here

Hooked
  • 84,485
  • 43
  • 192
  • 261
  • WOW. that's one cool answer you have there. So i assume that i need to use the Google Matrix ( or convert my graph into a matrix ) first before performing the hitting time algorithm ? – DjangoRocks Mar 09 '12 at 11:46
  • networkX has a pagerank method built in: http://networkx.lanl.gov/reference/algorithms.link_analysis.html – EdChum Mar 09 '12 at 14:09
  • @EdChum as I'm not exactly familiar with the pagerank algorithm, how is it related to mean first passage time (what I think the OP is calling hitting time)? I presented this solution as a pedagogic exercise to help anyone one solve the problem in general. Please post the networkx solution if you can show it solves the problem directly so I can see the proper way to solve it using the library. – Hooked Mar 09 '12 at 14:34
  • @DjangoRocks converting your graph to a matrix is simple, in fact I know that networkX has an output to edges: http://networkx.lanl.gov/reference/generated/networkx.convert.to_edgelist.html?highlight=edge%20list#networkx.convert.to_edgelist and one to a numpy matrix: http://networkx.lanl.gov/reference/generated/networkx.convert.to_numpy_matrix.html?highlight=matrix#networkx.convert.to_numpy_matrix – Hooked Mar 09 '12 at 14:35
  • It probably doesn't relate actually thinking about it as the pagerank includes a teleportation factor that computes the probability that you will escape a page that has no outlinks which is not what you want here as your final state is an absorbing one. @DjangoRocks why do you think PageRank is relevant here? Also MapReduce is just a technique to parallelise the computation of a taks across nodes in a network and it depends on your algorithm as to whether the tasks can be performed independently, is this true for what you are attempting? – EdChum Mar 09 '12 at 14:43
  • @EdChum ok this may sound stupid, but my professor explained the concept of hitting time using PageRank. so i thought Hitting Time is related to PageRank. – DjangoRocks Mar 10 '12 at 14:59