Dijkstra linear running time on dense graph with Binary Heap

Question

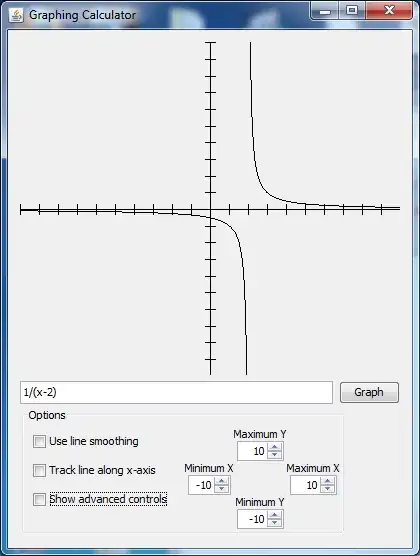
First: The general running time of Dijkstras Shortest Path algorithm is

where m is the number of edges and n the number of vertices

Second: the number of expected decreasekey operations is the following

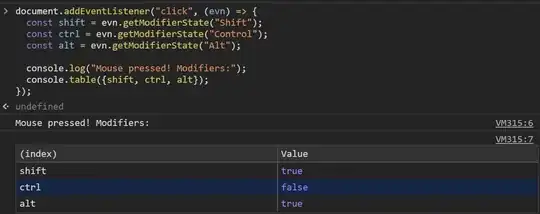
Third: The expected running time of dijkstra with a binary Heap which allows all operations in log(n) time is

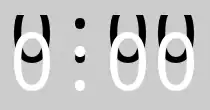
But why is the running time on dense graphs linear if we consider a graph dense if

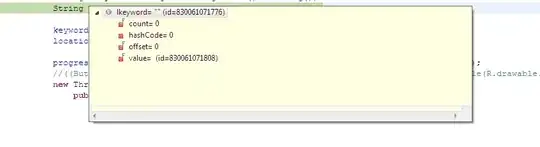
Can someone help with the O-notation and log calculations here?

Answer 1

my solution is now the following

Answer 2

First it isn't hard to show that if m is big omega of n log(n) log(log(n)) then log(n) is big omega of log(m). Therefore you can show that m is big omega of n log(m) log(log(m)).

From this you can show that n is big omega of m / (log(m) log(log(m))).

Substitute this back into the expression you have in the third point and we get that the expected running time is:

O(m + n log(m/n) log(n))

                   m                                                 m
    = O(m + (------------------) log(log(m) log(log(m))) log(------------------)
             log(m) log(log(m))                              log(m) log(log(m))

From here you can expand all of the logs of products into sums of logs. You'll get a lot of terms. And then it is just a question of demonstrating that every one is O(m) or o(m). Which is straightforward, though tedious.