8

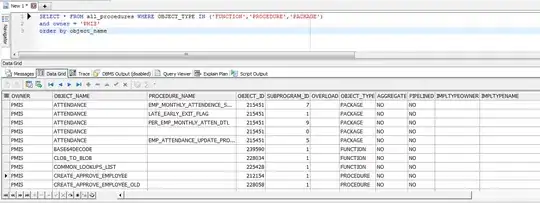
Instead of edge detection of a 2D image, I would like to detect edges on every single row (i.g. a line) of an image separately. That is detection of edges from an input 1D vector whose values are pixel intensities ranging from 0 to 255 ( image below): enter image description here

I would like to detect the major edges as appear in the sample input( image below) enter image description here

Cœur
  • 37,241
  • 25
  • 195
  • 267
C graphics
  • 7,308
  • 19
  • 83
  • 134
  • Thanks everyone for the responses. Please if you come across with any more new ideas(1Dimentional edge detections) share that here too. – C graphics Feb 15 '12 at 06:09

3 Answers3

10

One way to get to your desired result is to adapt the 2D Canny edge detector as follows (code in Mathematica):

First, compute the spatial derivative using a Gaussian derivative filter, setting the sigma value relative to the scale of the edges you want to detect. Take the absolute value of the result.

d = Abs@GaussianFilter[data, {{10, 5}}, 1];

Then, determine a threshold automatically to cluster the previous derivative values in two groups (here using Otsu's method).

thrd = FindThreshold[d];

Then, detect the steps of the derivative values (transitions into/from the "dead band").

steps = Flatten@Image`StepDetect[d, thrd]["NonzeroPositions"];

At this point you have the ends of the edges: 

ListLinePlot[data, Epilog -> {Red, PointSize[Large], Map[Point[{#, data[[#]]}] &, steps]}]

enter image description here

Optionally--it seems that's what you'd like--keep only the lowest ends of the edges. Clustering the data points at the ends of the edges works in this case, but I'm not sure how robust it is.

t = FindThreshold@data[[steps]];
steps2 = Select[steps, data[[#]] <= t &];

ListLinePlot[data, Epilog -> {Red, PointSize[Large], Map[Point[{#, data[[#]]}] &, steps2]}]

enter image description here

Matthias Odisio
  • 2,038
  • 12
  • 19
2

Given the nice contrast of these edges, there is an easy solution that will work robustly: detect all monotonous sequences of pixel values (strictly increasing or decreasing). You will keep the sequences having a total height above a threshold (50 in your case) to reject the noisy peaks.

As a byproduct, you'll get the starting and ending points (not exactly where you expect them though, but this can be improved on if needed).

Barcodes ?

1

So you are looking for a particular change in slope - ie a certain change in Y per sample?

Isn't it simply look at the difference in Y between two samples and if it's absolute value changed by more than some limit mark that as an edge?

Martin Beckett
  • 94,801
  • 28
  • 188
  • 263
  • 1
    No really, it would not be that simple at all. For the refrence look at : http://en.wikipedia.org/wiki/Edge_detection (Why edge detection is a non-trivial task) – C graphics Feb 13 '12 at 18:59
  • @Cgraphics: On the images you posted a simple difference or derivative of gaussian operator should work fine. If you think "it's not that simple at all", please post the actual data you're having trouble with. – Niki Feb 13 '12 at 19:27
  • @nikie that is the actual image, however it not as simple as a applying a simple threshold either. We need an accurate detection of edges not just, say, counting them. – C graphics Feb 13 '12 at 22:05