When I try to calculate the following integral in Mathematica 8, I get this strange result:
In[1]:= Integrate[y/((1 + x^2 + y^2)^(3/2)), {y, 0, 1}]
Maple 14 can solve this one easily:
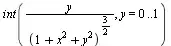
Why is Mathematica giving me a different result?
When I try to calculate the following integral in Mathematica 8, I get this strange result:
In[1]:= Integrate[y/((1 + x^2 + y^2)^(3/2)), {y, 0, 1}]

Maple 14 can solve this one easily:
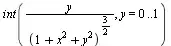

Why is Mathematica giving me a different result?
Try this
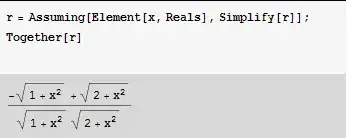
r = Integrate[y/((1 + x^2 + y^2)^(3/2)), {y, 0, 1}]
r = Assuming[Element[x, Reals], Simplify[r]];
Together[r]
which gives
(-Sqrt[1+x^2]+Sqrt[2+x^2])/(Sqrt[1+x^2] Sqrt[2+x^2])
Which is the same as Maple's :