3

I have to implement this algorithm in Mathematica:

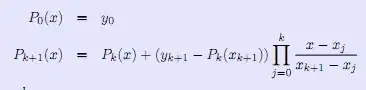
Algorithm

My problem is that I don't really understand the Mathematica syntax because there aren't a lot of useful examples out there. What I have done:

(* Input: 4 Points*)
Array[sx, 4, 0];
Array[sy, 4, 0];

sx[0] = -1; 
sy[0] = 0;

sx[1] = 0;
sy[1] = 2;

sx[2] = 1;
sy[2] = 4;

sx[3] = 3;
sy[3] = 32;


P[x,0]:=sy[0];

P[x, k_] := 
  P[x, k - 1] + (sy[k] - P[sx[k], k - 1])*
    Sum[(x - sx[j])/sx[k] - sx[j], {j, 0, x}];

(I tried to implement the geometric mean but I failed because I can't even calculate the Sum.)

How can I implement the recursion correctly? (an the geometric mean)

Brett Champion
  • 8,497
  • 1
  • 27
  • 44
ave4496
  • 2,950
  • 3
  • 21
  • 48

2 Answers2

3

You can define a function P like this :

P[x_, 0]  := sy[0] 
P[x_, k_] := P[x, k - 1] + (sy[k] - P[sx[k], k - 1])*
             Product[(x - sx[j])/(sx[k] - sx[j]), {j, 0, k - 1}] // Simplify

Setting values sx and sy as you defined above we get : 

In[13]:= P[x, 1] 
Out[13]= 2 (1 + x)

In[14]:= P[x, 2]
Out[14]= 2 (1 + x)

In[15]:= P[x, 3]
Out[15]= 2 + x + x^3
Artes
  • 1,133
  • 1
  • 17
  • 24
  • You are welcome, the method works just as a toy model, but the preferred way of interpolation in Mathematica is the method presented by Heike. – Artes Dec 27 '11 at 12:30
3

Just as an aside, Mathematica has a built-in function InterpolatingPolynomial. Suppose pts is the list of points for which you want to find the polynomial, then p[x, k] could be written as 

p[x_, k_] := InterpolatingPolynomial[pts[[;;k+1]] ,x]

For the example in the original post you would get

pts = {{-1, 0}, {0, 2}, {1, 4}, {3, 32}};

p[x, 0] // Simplify
p[x, 1] // Simplify
p[x, 2] // Simplify
p[x, 3] // Simplify

(* output
0
2 (1 + x)
2 (1 + x)
2 + x + x^3
*)
Heike
  • 24,102
  • 2
  • 31
  • 45