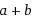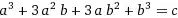1

I'd like to solve the following expression:

enter image description here

for the following equation:

equation

How? Is there a function for that. This was just an example.

  • Solve the expression means finds the value of the expression by substituting in the equation, so a+b = c^(1/3)

Thanks!!

  • 1
    Can you also give an example of what you expect the answer to be? – Greg Hewgill Dec 24 '11 at 05:24
  • 1
    Hmm, I doubt it. I can't see any way of generally doing this by hand either for non-trivial cases (`a + b = c^(1/3)` in this case). – Blender Dec 24 '11 at 05:24
  • I know how to do it by hand since it's easy, but there are equations that cannot be done by hand easily. That's why I thought there is a function for that !! –  Dec 24 '11 at 05:26
  • 3
    can you explain more what you mean by "solve the following expression"? one normally solves an "equation", not an "expression". I find the question not clear. – Nasser Dec 24 '11 at 06:05
  • Yeah, you can't solve an expression. Solving implies finding a set that satisfies a condition and an expression is not a condition. – David Z Dec 24 '11 at 07:19

2 Answers2

4

As pointed out in the comments, you can't solve an expression. But I'm guessing that what you meant to ask was how you can find the value of an expression (a+b) subject to a constraining equation (a^3 + 3 a^2 b + 3 a b^2 + b^3 == c). In general, that's not possible - that is, for an arbitrary expression subject to an arbitrary constraint, there's no guarantee that the expression will have the same value at all the points satisfied by the constraint.

What you can do sometimes is this: introduce a new variable to represent the value of your expression, solve the resulting equation for one of the original variables (perhaps manually), then substitute it into the condition. For example, in this case:

  1. Let x represent the value of a + b
  2. Solve the equation a + b == x for either a or b, giving a = x - b or b = x - a

  3. Substitute either of these into the condition,

    a^3 + 3 a^2 b + 3 a b^2 + b^3 == c /. a -> x-b // FullSimplify

If your expression (a + b) has a value that is constant over the solution set of the condition, and if Mathematica is able to simplify it, then you'll get a result that is independent of any of the variables in the expression (a and b). In this example you get the result c == x^3, so that is the case.

David Z
  • 128,184
  • 27
  • 255
  • 279
3

It is not clear to me what you what, but I am going to take a guess and hope this helps.

expr = a + b;
eq = a^3 + 3 a^2 b + 3 a b^2 + b^3 == c;

PolynomialReduce[Subtract @@ eq, expr];

expr == FullSimplify[ -%[[2]] / %[[1, 1]] ]

Output:

a + b == c/(a + b)^2

This relies on PolynomialReduce and therefore only works with polynomial equations.

Mr.Wizard
  • 24,179
  • 5
  • 44
  • 125
  • Assuming the equations are polynomial (so that `Solve` is ok to use) and taking the same guess `(a+b)/.Solve[eq,{a,b}]` gives the desired results for the example: `{c^(1/3), -(1/2) (1 - I Sqrt[3]) c^(1/3), -(1/2) (1 + I Sqrt[3]) c^( 1/3)}`. For general polynomials that involve variables `a,b,c` the result given for `a+b` will be a function of b and c. To get `a+b` as a function of a and c, use `(a+b)/.Solve[eq,{b,a}]` . – kglr Dec 24 '11 at 07:53