How do I enumerate and deduplicate 9 items allocated in triplets to each of 3 inheritors... and beyond?

Question

This question is related to the context described in Seeking a solution or a heursitic approxmation for the 3-partition combinatorial situation. The task is distribute approximately 48 pieces of inherited jewelry, each with its appraised value, to 3 inheritors so as to give each inheritor equal or nearly equal value. That question has been sufficiently answered for my legalistic purposes.

This new question arises out of my pursuit of solving this by enumeration. Totally unnecessary legally. Just an intellectual challenge now.

The problem now:

Assign to each item a unique index: probably just the integers 1 through 48. Now allocate these 48 to each of the 3 inheritors and eliminate the duplicates.

To make this example case simpler, assert that there are only 9 items and each inheritor is to receive exactly 3 items. (Note that this diverges from the previous goal of making the 3 bins of nearly equal value.)

How to eliminate the duplications in the sequence of items-to-bins?

Example:
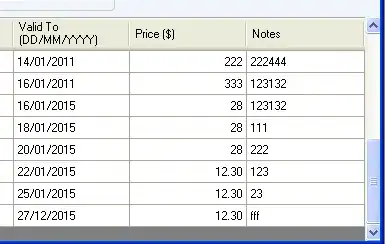
Let bin 1 contain items {1,2,3}
Let bin 2 contain items {4,5,6}
Let bin 3 contain items {7,8,9}

There will be 6 duplications of the final values of this triplet-of-triplets:
{1,2,3}{4,5,6}{7,8,9}
{4,5,6}{1,2,3}{7,8,9}
{4,5,6}{7,8,9}{1,2,3}
{7,8,9}{1,2,3}{4,5,6}
{7,8,9}{4,5,6}{1,2,3}
etc.

Again, how to eliminate the duplications in the sequence of items-to-bins? Without enumerating the entire set of permutations-of-triplets. No, that's not quite right. I might have to temporarily grind out all the permutations-of-triplets. How to quickly eliminate the duplicated combinations-of-triplets based on what has been done a priori?

I can imagine something like inventing a function which, given any combination of 3 items, returns a unique value. Something using prime numbers? Except that many pairs of prime numbers sum to another prime number.

I crossposted the original question on mathoverflow. I apologize for not understanding the relationship between stackoverflow and mathoverflow.

Answer 1

One can show that the total number of restricted partitions is

, which equals 280.

This can be reordered as:

You can get this by taking the first third of the (ordered) combinations you obtain by taking three out of nine list members and the first half of the combinations you get when you take three out of the remaining six for each choice of the first three. There's no free choice for the last three of course.

With Mathematica you might generate this as:

list = Range[9];
l1 = Subsets[list, {3}, Binomial[9, 3]/3];
l2 = Subsets[Complement[list, #], {3}, Binomial[6, 3]/2] & /@ l1;
Flatten[
  Outer[
    Function[{ll1, ll2}, {ll1, ll2, Complement[list, ll1, ll2]}], 
    {#1}, #2, 1, 1
  ] & @@@ ({l1, l2}\[Transpose]), 
2]

Answer 2

This is a good question. It is essentially a restricted set partition problem.

Here is one way in which you may approach this. I am not certain that it is optimal, but it is many magnitudes more efficient than brute force (generating all permutations and then removing duplicates).

I will be using curly brackets to represent lists, as this is familiar to me.

Start with this template, which represents zero items in three bins:

{ {{}, {}, {}} }

For each list within the outermost (i.e. just {{}, {}, {}} here):

1. Append 1 to each sub-list, skipping any lists that are full (contain three elements), and append only to the first empty {} list if there is more than one.

2. Keep a copy of the entire list for each replacement that is made, and join these together at the end of the step.

This process will then be repeated for 2, 3, etc., until all items are in bins or all bins are full. Example steps:

{ {{}, {}, {}} }

{ {{1}, {}, {}} }

{ {{1, 2}, {}, {}}, {{1}, {2}, {}} }

{ {{1, 2, 3}, {}, {}}, {{1, 2}, {3}, {}}, {{1, 3}, {2}, {}}, {{1}, {2, 3}, {}}, {{1}, {2}, {3}} }

{ {{1, 2, 3}, {4}, {}}, {{1, 2, 4}, {3}, {}}, {{1, 2}, {3, 4}, {}}, {{1, 2}, {3}, {4}}, {{1, 3, 4}, {2}, {}}, {{1, 3}, {2, 4}, {}}, {{1, 3}, {2}, {4}}, {{1, 4}, {2, 3}, {}}, {{1}, {2, 3, 4}, {}}, {{1}, {2, 3}, {4}}, {{1, 4}, {2}, {3}}, {{1}, {2, 4}, {3}}, {{1}, {2}, {3, 4}} }