Equation from "Programming Pearls" - can somebody explain me?

Question

It's feel like I'm stuck, my friends. Can somebody explain me pick equations from "Pearls of Functional Algorithm Design", chapter 11 ("Not the maximum segment sum").

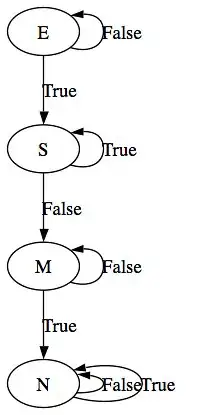
Here is the problem (a little bit simplified) Let us have some states with given transitions:

data State = E | S | M | N 
                deriving (Show, Eq) 

step E False = E 
step E True = S 
step S False = M 
step S True = S 
step M False = M 
step M True = N 
step N False = N 
step N True = N 

Now, let's define pick:

 pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

The author claims that the following seven equations hold:

pick E xs = [[]]
pick S [ ] = [ ]
pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs)
pick M [ ] = [ ]
pick M (xs ++ [x ]) = pick M xs ++ pick S xs
pick N [ ] = [ ]
pick N (xs ++ [x]) = pick N xs ++ map (++[x]) (pick N xs ++ pick M xs)

Can somebody explain me in simple words, why these equations are true, how can we prove an obvious proof? I feel like I almost understand S-equations, but altogether this remains elusive.

Answer 1

Ok, I needed to visualize your state graph:

And give a type signature for pick :: State -> [[Bool]] -> [(State, [Bool]).

Now, this doesn't jive with your first equation pick E xs = [[]] - it'd have to be pick E xs = [(E,[])].

Perhaps you meant to define pick this way:

pick :: State -> [[Bool]] -> [[Bool]]
pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

Assuming that definition, the first equation now makes sense. It claims that if you start at E, the only sequence of booleans in xs that will end at E is the empty list.

Note that this assumes that [] ∈ xs.

Also, if ys = replicate n False, pick E [ys] = [ys], so this implies that ∀ n, ys ∉ xs.

The second, fourth, and sixth equations are all of the form pick _ [ ] = [ ], which is trivially true by the definition of map and filter.

The third equation, pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs) doesn't really make sense either. What I'm guessing it's trying to say is:

pick S (map (++[True] xs) = map (++[True]) (pick S xs ++ pick E xs)

Which is to say - any path starting at E and ending at S can be constructed by taking an existing path to E or S and appending True. Equivalently, that every path that ends at S must end with True.

The fifth equation is similarly nonsensical, and should be stated as:

pick S (map (++[False] xs) = map (++[False]) (pick S xs ++ pick M xs)

And the seventh equation should be restated as:

pick N (map (++ [True]) xs) = pick N xs ++ map (++[True]) (pick N xs ++ pick M xs)