1)a workaround for "NMaximize" error "function unbounded." but don't know why 2) more importantly, how to speed up this 3d region plot (see update2)

Question

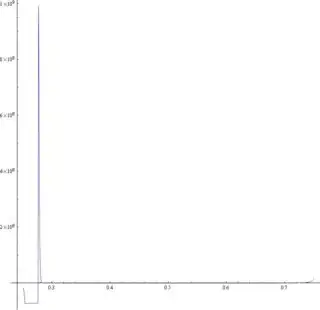
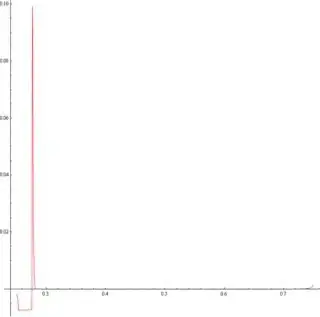
When I was trying to find the maximum value of f using NMaximize, mathematica gave me a error saying

NMaximize::cvdiv: Failed to converge to a solution. The function may be unbounded.

However, if I scale f with a large number, say, 10^5, 10^10, even 10^100, NMaximize works well.

In the two images below, the blue one is f, and the red one is f/10^10.

Here come my questions:

Is scaling a general optimization trick?
Any other robust, general workarounds for the optimizations such needle-shape functions?
Because the scaling barely changed the shape of the needle-shape of f, as shown in the two images, how can scaling work here?

thanks :)

Update1: with f included

Clear["Global`*"]

d = 1/100;
mu0 = 4 Pi 10^-7;
kN = 97/100;
r = 0.0005;
Rr = 0.02;
eta = 1.3;

e = 3*10^8;

s0 = 3/100;

smax = 1/100; ks = smax/s0;
fre = 1; tend = 1; T = 1;
s = s0*ks*Sin[2*Pi*fre*t];
u = D[s, t];
umax = N@First[Maximize[u, t]];

(*i=1;xh=0.1;xRp=4.5`;xLc=8.071428571428573`;
i=1;xh=0.1;xRp=4.5;xLc=8.714285714285715;*)
i = 1; xh = 0.1; xRp = 5.5; xLc = 3.571428571428571`;
(*i=1;xh=0.1`;xRp=5.`;xLc=6.785714285714287`;*)

h = xh/100; Rp = xRp/100; Lc = xLc/100;
Afai = Pi ((Rp + h + d)^2 - (Rp + h)^2);
(*Pi (Rp-Hc)^2== Afai*)
Hc = Rp - Sqrt[Afai/Pi];
(*2Pi(Rp+h/2) L/2==Afai*)
L = (2 Afai)/(\[Pi] (h + 2 Rp));
B = (n mu0 i)/(2 h);

(*tx = -3632B+2065934/10 B^2-1784442/10 B^3+50233/10 B^4+230234/10 \
B^5;*)
tx = 54830.3266978739 (1 - E^(-3.14250266080741 B^2.03187556833859));

n = Floor[(kN Lc Hc)/(Pi r^2)] ;

A = Pi*(Rp^2 - Rr^2);
b = 2*Pi*(Rp + h/2);

(* -------------------------------------------------------- *)

Dp0 = 2*tx/h*L; 


Q0 = 0;

Q1 = ((1 - 3 (L tx)/(Dp h) + 4 (L^3 tx^3)/(Dp^3 h^3)) Dp h^3)/(
   12 eta L) b;
Q = Piecewise[{{Q1, Dp > Dp0}, {Q0, True}}];


Dp = Abs[dp[t]];


ode = u A - A/e ((s0^2 - s^2)/(2 s0 )) dp'[t] == Q*Sign[dp[t]];

sol = First[
   NDSolve[{ode, dp[0] == 0}, dp, {t, 0, tend} , 
    MaxSteps -> 10^4(*Infinity*), MaxStepFraction -> 1/30]];

Plot[dp''[t] A /. sol, {t, T/4, 3 T/4}, AspectRatio -> 1, 
 PlotRange -> All]
Plot[dp''[t] A /10^10 /. sol, {t, T/4, 3 T/4}, AspectRatio -> 1, 
 PlotRange -> All, PlotStyle -> Red]

f = dp''[t] A /. sol;
NMaximize[{f, T/4 <= t <= 3 T/4}, t]
NMaximize[{f/10^5, T/4 <= t <= 3 T/4}, t]
NMaximize[{f/10^5, T/4 <= t <= 3 T/4}, t]
NMaximize[{f/10^10, T/4 <= t <= 3 T/4}, t]

update2: Here comes my real purpose. Actually, I am trying to make the following 3D region plot. But I found it is very time consuming (more than 3 hours), any ideas to speed up this region plot?

Clear["Global`*"]

d = 1/100;
mu0 = 4 Pi 10^-7;
kN = 97/100;
r = 0.0005;
Rr = 0.02;
eta = 1.3;

e = 3*10^8;

s0 = 3/100;

smax = 1/100; ks = smax/s0;
f = 1; tend = 1/f; T = 1/f;
s = s0*ks*Sin[2*Pi*f*t];
u = D[s, t];
umax = N@First[Maximize[u, t]];


du[i_?NumericQ, xh_?NumericQ, xRp_?NumericQ, xLc_?NumericQ] := 
 Module[{Afai, Hc, L, B, tx, n, A, b, Dp0, Q0, Q1, Q, Dp, ode, sol, 
   sF, uF, width, h, Rp, Lc},
  h = xh/100; Rp = xRp/100; Lc = xLc/100;
  Afai = Pi ((Rp + h + d)^2 - (Rp + h)^2);

  Hc = Rp - Sqrt[Afai/Pi];

  L = (2 Afai)/(\[Pi] (h + 2 Rp));
  B = (n mu0 i)/(2 h);


  tx = 54830.3266978739 (1 - E^(-3.14250266080741 B^2.03187556833859));

  n = Floor[(kN Lc Hc)/(Pi r^2)] ;

  A = Pi*(Rp^2 - Rr^2);
  b = 2*Pi*(Rp + h/2);

  Dp0 = 2*tx/h*L;  


  Q0 = 0;

  Q1 = ((1 - 3 (L tx)/(Dp h) + 4 (L^3 tx^3)/(Dp^3 h^3)) Dp h^3)/(
    12 eta L) b;
  Q = Piecewise[{{Q1, Dp > Dp0}, {Q0, True}}];

  Dp = Abs[dp[t]];


  ode = u A - A/e ((s0^2 - s^2)/(2 s0 )) dp'[t] == Q*Sign[dp[t]];

  sol = First[
    NDSolve[{ode, dp[0] == 0}, dp, {t, 0, tend} , MaxSteps -> 10^4, 
     MaxStepFraction -> 1/30]];


  sF = ParametricPlot[{s, dp[t] A /. sol}, {t, 0, tend}, 
    AspectRatio -> 1];


  uF = ParametricPlot[{u, dp[t] A /. sol}, {t, 0, tend}, 
    AspectRatio -> 1];


  tdu = NMaximize[{dp''[t] A /10^8 /. sol, T/4 <= t <= 3 T/4}, {t, 
     T/4, 3 T/4}, AccuracyGoal -> 6, PrecisionGoal -> 6];

  width = Abs[u /. tdu[[2]]];

  {uF, width, B}]

RegionPlot3D[
 du[1, h, Rp, Lc][[2]] <= umax/6, {h, 0.1, 0.2}, {Rp, 3, 10}, {Lc, 1, 
  10}, LabelStyle -> Directive[18]]

@David and Mr Wizard, thanks for your kindly concern. I thought it would be a little nasty to show `f` here. :). OK, I made two updates now. — FreshApple, Oct 19 '11 at 23:42
Scaling or normalization is quite a standard technique in optimization. — PlatoManiac, Oct 19 '11 at 23:53
@PlatoManiac, thank you very much. Would you please give me some suggestions on the question in my update2 above? :) — FreshApple, Oct 19 '11 at 23:57
@FreshApple that is a little overwhelming I admit, but at least now there is something to sink our teeth into. — Mr.Wizard, Oct 20 '11 at 00:10
First question: why are there `ParametricPlot` call inside `du`? — Mr.Wizard, Oct 20 '11 at 00:11

score 0 · Answer 1 · answered Oct 20 '11 at 04:24

NMaximize::cvdiv is issued if the optimum improved a couple of orders of magnitude during the optimization process, and the final result is "large" in an absolute sense. (To prevent the message in a case where we go from 10^-6 to 1, for example.)

So yes, scaling the objective function can have an effect on this.

Strictly speaking this message is a warning, and not an error. My experience is that if you see it, there's a good chance that your problem is unbounded for some reason. In any case, this warning is a hint that you might want to double check your system to see if that might be the case.

1)a workaround for "NMaximize" error "function unbounded." but don't know why 2) more importantly, how to speed up this 3d region plot (see update2)

1 Answers1