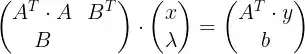Constrained Least Squares with Numpy and Python only

Question

How to do constrained Least Squares only using numpy. Is there any way to incorporate constraints into numpy.linalg.lstsq() or is there any numpy+Python workaround to do constrained Least Squares? I know that I can do this easily with cvxpy and scipy.optimize, but this optimization will be a part of numba JITed function, and those two are not supported by numba.

EDIT: Here is a dummy example of a problem I want to solve

arr_true = np.vstack([np.random.normal(0.3, 2, size=20),
                      np.random.normal(1.4, 2, size=20),
                      np.random.normal(4.2, 2, size=20)]).transpose()
x_true = np.array([0.3, 0.35, 0.35])
y = arr_true @ x_true

def problem():
    noisy_arr = np.vstack([np.random.normal(0.3, 2, size=20),
                        np.random.normal(1.4, 2, size=20),
                        np.random.normal(4.2, 2, size=20)]).transpose()

    x = cvxpy.Variable(3)
    objective = cvxpy.Minimize(cvxpy.sum_squares(noisy_arr @ x - y))
    constraints = [0 <= x, x <= 1, cvxpy.sum(x) == 1]
    prob = cvxpy.Problem(objective, constraints)
    result = prob.solve()
    output = prob.value
    args = x.value

    return output, args

Essentially, my problem is to minimize $Ax-y$ subject to $x_1+x_2+x_3 = 1$ and $\forall x_i, 0 \leq x_i \leq 1$.

Can you provide an example and or explain what is the type of constraints you have? — WArnold, Jul 27 '23 at 16:11
At the very least, you should be able to write your constraints as a penalty or merit function, and sum it with the original objective function. Have you defined the KKT conditions for your problem? If so, solve that system in order to get a solution for your problem. You could also try QR-factorization or Lagrange multipliers (least norm problem). It really depends on your specific problem. Are you looking for a solution, or a specific method to find the solution? — Michael Ruth, Jul 27 '23 at 17:15
Please should your work / what you have tried. Please also read [ask]. — BadZen, Jul 27 '23 at 17:36
@jared you can JIT both `np.linalg.lstsq` and `np.linalg.solve` numba — cc88, Jul 29 '23 at 02:29

Dr. V · Answer 1 · 2023-07-27T17:33:20.750

3

Is it linear? Based on your numpy.linalg.lstsq suggestion I'll assume that for now. Also, I assume (to solve the simple case first) that you talk about equality constraints. Then you can easily solve it yourself by using Lagrange multipliers, and the solution can be found by solving a linear equation system.

If the problem is to minimize A * x - y over the constraints B * x = b, then solve

$\begin{pmatrix}A^T\cdot A&B^T\\B&\end{pmatrix}\cdot\begin{pmatrix}x\\\lambda\end{pmatrix}=\begin{pmatrix}A^T\cdot y\\b\end{pmatrix}$

As an example:

from numpy import array, zeros
from numpy.linalg import solve

A = array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = array([3.2, 6.8, 11.1, 15.2])

B = array([[1, -1]])
b = array([0.1])

S = zeros((3, 3))
r = zeros(3)

S[:2, :2] = A.T @ A
S[2:, :2] = B
S[:2, 2:] = B.T
r[:2] = A.T @ y
r[2] = b

x = solve(S, r)[:2]
print(x)

Disclamer: Bugs might be included, but brief testing gave me for x

[1.06262376 0.96262376]

This seems reasonable, and my constraint x1 - x2 = 0.1 is also fulfilled.

edited Jul 27 '23 at 17:33

answered Jul 27 '23 at 17:15

Dr. V

1,747
1
11
14

thanks, this is great! i've updated the question with an example, please take a look. two questions: 1) what to do when you have inequality constraints, and 2) can you explain or point me to a resource about how you set up this Lagrange system in matrix form? – cc88 Jul 29 '23 at 02:35
1

Sorry, @cc88, while I had the case of equality constraints in my head, I never seriously coded handling of inequality constraints myself. Also for the second question, look for multivariable optimization with Lagrange multipliers. This is really an optimization (minimization) of `(A*x - y)**2`. – Dr. V Jul 29 '23 at 13:36

Constrained Least Squares with Numpy and Python only

1 Answers1