If I am not mistaken, you are trying to implement this paper.
I am giving you a rough sketch on how to implement the objective mentioned by you in question. You can try and implement the other two objectives in similar manner. To implement maximize for the third objective just take the negative of the objective and pass to minimize function.
PS I am using python 3.8.10 with pymoo 0.6.0 to code this example. This is to illustrate how to implement it in pymoo. For exact/correct solution you may have to consider the data and implement other objectives mentioned in the paper.
from pymoo.core.problem import Problem
from pymoo.operators.crossover.sbx import SBX
from pymoo.operators.mutation.pm import PM
from pymoo.operators.repair.rounding import RoundingRepair
from pymoo.operators.sampling.rnd import IntegerRandomSampling
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.optimize import minimize
import numpy as np
C = np.array([[1,2,3], [4,5,6], [7,8,9], [10,11,12]])
PCI = np.array([[2,1,3], [4,6,5], [9,7,8], [12,10,11]])
W = np.array([2,5,7])
L = np.array([3,5,4])
T = 20
class PavementProblem(Problem):
def __init__(self, C, PCI, W, L, T, PCImin, **kwargs):
n_var = C.shape[0]*C.shape[1]
# n_var, n_obj, n_ieq_constr, xl, xu, vtype,
self.C = C
self.PCI = PCI
self.PCImin = PCImin
self.W = W
self.L = L
n_ieq = PCI.shape[0]*PCI.shape[1]
super().__init__(n_var=n_var, n_obj=3, n_ieq_constr=n_ieq, xl=1, xu=T, vtype=int, **kwargs)
def _evaluate(self, x, out, *args, **kwargs):
x2d = x.reshape(self.C.shape[0], self.C.shape[1]) # some transformation to convert linear x to x2d
obj_list = []
Cx = np.multiply(self.C, x2d)
# Objective mentioned in the question by OP
obj1 = np.einsum('ij,j->', Cx, self.W*self.L)
# Create other objectives and append them to obj_list
obj_list.append(obj1)
out["F"] = np.column_stack(obj_list)
pci = self.PCImin - self.PCI # implement greater-than-equal-to in pymoo
# flattened the 2d array so that each element will act as a constraint.
out["G"] = np.column_stack(pci.flatten())
problem = PavementProblem(C, PCI, W, L, T, 8)
algorithm = NSGA2(pop_size=200, sampling=IntegerRandomSampling(),
crossover=SBX(prob=1.0, eta=3.0, vtype=float, repair=RoundingRepair()),
mutation=PM(prob=1.0, eta=3.0, vtype=float, repair=RoundingRepair()), eliminate_duplicates=True)
res = minimize(problem, algorithm, ('n_gen', 200), seed=1, verbose=False, return_least_infeasible=True)
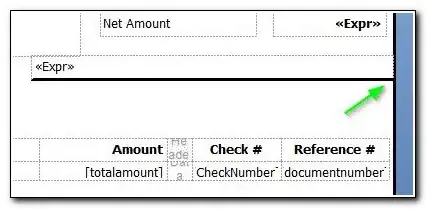 , one of the objective functions is:
, one of the objective functions is: