I'm using wavelet transform to denoise a signal and I've implemented dwt in c trying to replicate the python library pywavelets but doing additional levels of wavelet transform doesn't seem to remove low frequency events compared to the python library. The blue signal is the raw data and the orange is the denoised signal. If you look at the resulting denoised signals, my transformations starts removing more signal peaks than noise.
1st lvl transformation:
[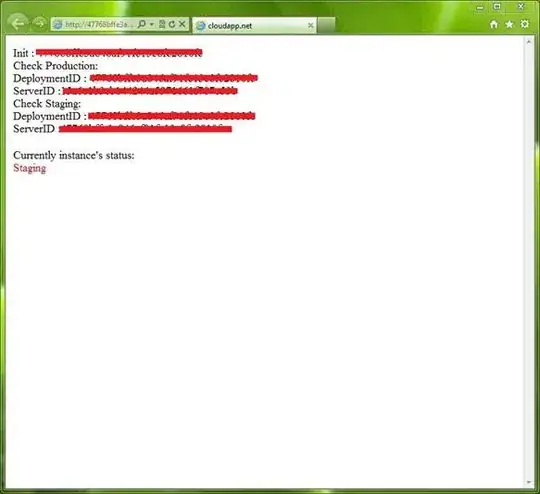 ]
]
2nd lvl transformation:
[ ]
]
3rd lvl transformation:
[ ]
]
4th lvl transformation:
[ ]
]
4th lvl transform with pywavelet:
[ ]
]
The noise using the python library is a lot cleaner compared to my signals.
Can someone familiar with wavelet transform spot any issues with my code?
void forward(float* arrTime, float* out, int size) {
int h = size >> 1; // .. -> 8 -> 4 -> 2 .. shrinks in each step by half wavelength
for( int i = 0; i < h; i++ ) {
out[ i ] = out[ i + h ] = 0; // set to zero before sum up
for( int j = 0; j < _motherWavelength; j++ ) {
int k = ( i << 1 ) + j; // k = ( i * 2 ) + j;
while( k >= size)
k -= size; // circulate over arrays if scaling and wavelet are are larger
out[ i ] += arrTime[ k ] * _scalingDeCom[ j ]; // low pass filter for the energy (approximation)
out[ i + h ] += arrTime[ k ] * _waveletDeCom[ j ]; // high pass filter for the details
} // Sorting each step in patterns of: { scaling coefficients | wavelet coefficients }
} // h = 2^(p-1) | p = { 1, 2, .., N } .. shrinks in each step by half wavelength
} // forward
void threshold(float* coeffs, int size)
{
// soft thresholding
float sigma = 10e-4;
float thres = sigma * sqrt(2 * log(size));
for (int i = (size >> 1); i < size; i++)
{
if (abs(coeffs[i]) < thres)
{
coeffs[i] = 0;
} else {
coeffs[i] = (coeffs[i]/abs(coeffs[i])) * (abs(coeffs[i]) - thres);
}
}
}
void reverse(float* arrHilb, float* out, int size) {
for( int i = 0; i < (sizeof(out)/sizeof(float)); i++ )
out[ i ] = 0; // set to zero before sum up
int h = size >> 1; // .. -> 8 -> 4 -> 2 .. shrinks in each step by half wavelength
for( int i = 0; i < h; i++ ) {
for( int j = 0; j < _motherWavelength; j++ ) {
int k = ( i << 1 ) + j; // k = ( i * 2 ) + j;
while( k >= size )
k -= size; // circulate over arrays if scaling and wavelet are larger
// adding up energy from low pass (approximation) and details from high pass filter
out[ k ] +=
( arrHilb[ i ] * _scalingReCon[ j ] )
+ ( arrHilb[ i + h ] * _waveletReCon[ j ] ); // looks better with brackets
} // Reconstruction from patterns of: { scaling coefficients | wavelet coefficients }
} // h = 2^(p-1) | p = { 1, 2, .., N } .. shrink in each step by half wavelength
} // reverse