Removing the penalty on the quadratic term in a penalized cubic spline in MGCV?

Question

I'd like to fit a penalized cubic spline with the R package mgcv in which I don't apply any penalty to the intercept, linear, AND quadratic terms in the model. The penalty should only apply to the cubic and other terms in the spline basis. I'd like to fit my model this way because the standard in my field is to use a quadratic term to adjust for x in some code like lm(y~x+x^2). I believe that there could be moderate departures from this model in my data, so I would like to fix a more flexible (but not too wiggly) model, and hence use the penalized splines.

It is my current understanding that mgcv will automatically place no penalty on the intercept and linear term, but the quadratic term will be penalized.

So, if my working model can be fit with the following code

x <- seq(0,1, length = 100)
y <- 0.5*x + x^2 + rnorm(100)
mod1 <- gam(
    y~s(x, fx = F, k = 5, bs = "cr")
)

then calling mod1$coefficients yields a vector of length 5, representing the intercept, linear term, quadratic term, cubic term, and one cubic spline term. Hence, it is my current understanding that mod1$coefficients[1:2] are not penalized and mod1$coefficients[3:5] are penalized. Is my understanding correct? If so, how might I modify the code above to remove the penalty in the estimation of mod1$coefficients[3]?

I have tried toying with the parameter m within the spline function s(), as the mgcv documentation indicates that this will alter the derivative of the spline function on which the penalty is placed. However, this doesn't seem to alter the fitted spline at all.

mod1 <- gam(
    y~s(x, fx = F, k = 10, bs = "cr")
)
mod2 <- gam(
    y~s(x, fx = F, k = 10, bs = "cr", m = c(3,3))
)
all(mod1$fitted.values == mod2$fitted.values) # this is always true

Answer 1

It's not a cubic regression spline, but it does clearly separate the two components of your problem. Here I show how to do this with a thin plate spline, the default basis in mgcv::gam().

Using your setup plus my package for working with GAMs

library("mgcv")
library("gratia")
library("ggplot2")

set.seed(1)
df <- data.frame(x = seq(0,1, length = 100),
                 y = 0.5*x + x^2 + rnorm(100))

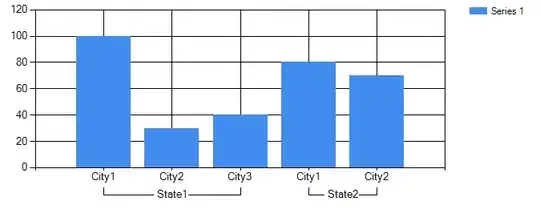
we begin by looking at the basis for a thin plate spline with a 3rd derivative penalty:

basis(s(x, m = 3), data = df) |>
  draw() +
  facet_wrap(~ bf)

which results in

The last three basis functions (9, 10, & 11) are in the null space of the penalty; they are not affected by the penalty because they have 0 third derivative everywhere. Function 11 is a quadratic term. Function 9 is confounded with the model intercept and will be removed from the basis via the imposition of a sum-to-zero constraint on the basis; this is the default constraint and gam() does this by default when fitting a GAM.

The GAM you want to fit (assuming a thin plate spline is OK) then is

m <- gam(y ~ s(x, m = 3), data = df, method = "REML")
summary(m)

The model uses 2 EDF as we would expect given the way the data has been simulated

> summary(m)                                                                  

Family: gaussian 
Link function: identity 

Formula:
y ~ s(x, m = 3)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.6939     0.0907   7.651 1.47e-11 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
     edf Ref.df    F  p-value    
s(x)   2      2 11.1 4.56e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

R-sq.(adj) =   0.17   Deviance explained = 18.6%
-REML = 134.45  Scale est. = 0.82259   n = 100

If you want a formal test of the spline bit over the order 2 polynomial terms, then we can refit the model above but including the required terms as parametric terms via poly(x, 2) but modify the basis of the thin plate spline to get rid of all the functions in the penalty null space. We remove the null space by setting m = c(3,0):

basis(s(x, m = c(3, 0)), data = df) |>
  draw() +
  facet_wrap(~ bf)

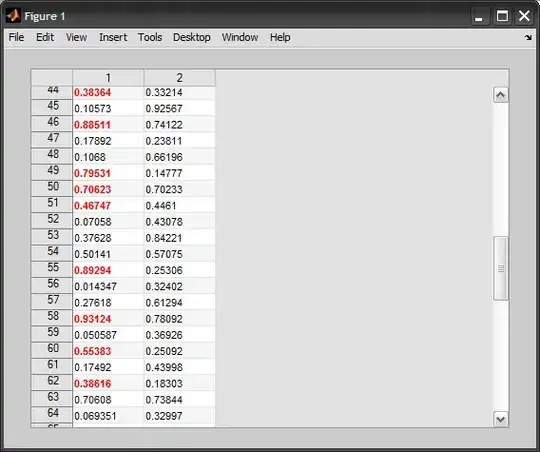
Notice how functions 9, 10, and 11 are no longer found in the basis. This is what will allow us to isolate the wiggliness-beyond-quadratic component in the spline, leaving the order-2-polynomial-wiggliness to the parametric terms in the model.

m0 <- gam(y ~ poly(x, 2) + s(x, m = c(3, 0)), data = df, method = "REML")
summary(m0)

The last line produces

> summary(m0)                                                                 

Family: gaussian 
Link function: identity 

Formula:
y ~ poly(x, 2) + s(x, m = c(3, 0))

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.6939     0.0907   7.651 1.47e-11 ***
poly(x, 2)1   4.2437     0.9113   4.657 1.02e-05 ***
poly(x, 2)2   0.5129     0.9074   0.565    0.573    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
           edf Ref.df F p-value
s(x) 0.0001194      8 0    0.72

R-sq.(adj) =   0.17   Deviance explained = 18.6%
-REML = 130.47  Scale est. = 0.82259   n = 100

And as we'd already seen, the beyond-quadratic wiggliness is tiny and we fail to reject the null hypothesis that the f(x) === 0.

---

I think you can do this using the B spline basis, which allows you to control the order of the polynomial and the order of the penalty (unlike the cubic regression spline basis, which is fixed to be formed from piecewise cubic polynomials, with 2nd order derivative penalty):

# make it mildly cubic
set.seed(1)
df2 <- data.frame(x = seq(0,1, length = 100),
                  y = 0.5*x + x^2 + (0.1 * (x^3)) + rnorm(100))

m1 <- gam(y ~ s(x, bs = "bs", m = c(3,3)),
          data = df2, method = "REML")

This will penalise functions with non-zero third derivative so shouldn't be penalising the linear and quadratic functions in the span of the basis. It's just much less clear how it is doing this, and you certainly can't interpret the coefficients in the way you assumed for the CRS (you can't interpret them that way for the bs = "cr" basis either - plot the basis functions for s(x, bs = "cr") to see why). This is what the fitted basis functions look like for m1 with the B spline basis

basis(m1) |>
  draw()

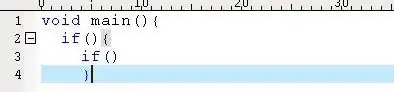
The fitted functions have to look like because the estimated spline is:

draw(m1)

Answer 2

Here's an appoach to adding a cubic term to a quadratic model:

> x <- seq(0,1, length = 100)
> y <- 0.5*x + x^2 + rnorm(100)
> mod1 <- gam(
+     y~s(x, fx = F, k = 3, bs = "cr")+ I(x^3)
+ )
> mod1$coefficients
(Intercept)      I(x^3)      s(x).1      s(x).2 
-1.70442708  9.32342373  0.03978659 -5.49355285 
> summary(mod1)

Family: gaussian 
Link function: identity 

Formula:
y ~ s(x, fx = F, k = 3, bs = "cr") + I(x^3)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)   -1.704      1.014  -1.680   0.0961 .
I(x^3)         9.323      3.999   2.331   0.0218 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
     edf Ref.df     F p-value
s(x) 1.8   1.96 1.925   0.125

R-sq.(adj) =  0.255   Deviance explained = 27.6%
GCV = 0.94177  Scale est. = 0.90598   n = 100

Here's the output of plot:

png( ); plot(mod1) ; dev.off()

Compare with:

> mod2 <- gam(
+     y~s(x, fx = F, k = 3, bs = "cr")
+ )
> summary(mod2)

Family: gaussian 
Link function: identity 

Formula:
y ~ s(x, fx = F, k = 3, bs = "cr")

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.64997    0.09781   6.646 1.74e-09 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
       edf Ref.df     F  p-value    
s(x) 1.433  1.679 14.62 1.35e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

R-sq.(adj) =  0.213   Deviance explained = 22.4%
GCV = 0.98046  Scale est. = 0.9566    n = 100
> png( ); plot(mod2) ; dev.off()
quartz 
     2