How to approximate an ellipse from the exterior?

Question

In order to solve this problem about the overlap of two ellipses, we approximate the ellipses from their interior. Indeed an ellipse is convex and we construct a path by joining successive points on the perimeter. This gives a polygon contained in the ellipse.

So the area we find at the end is necessarily less than the true area: we get a lower bound of the area.

How to construct a polygon containing the ellipse (and approximating it of course), in order to get an upper bound? It does not seem easy to construct an envelope by taking small pieces of tangents.

user2554330 · Accepted Answer · 2023-05-10T23:02:28.243

Constructing the tangents isn't too hard, using the ellipse formula given in this answer. It gives the ellipse in parametric form; to get the slopes of the tangents, use (dy/dtheta)/(dx/dtheta), i.e.

slopes <- (-a * sin(theta) * sin(angle) + b * cos(theta) * cos(angle))/
            (-a * sin(theta) * cos(angle) - b * cos(theta) * sin(angle))

Then the intercepts come from intercepts <- y - slopes*x, where x and y are from points on the ellipse.

Finally, you would intersect successive pairs of those tangent lines to get the vertices of the outer polygon. Here's a complete solution:

innerouter <- function(x0, y0, a, b, angle, n = 360) {
    angle <- angle/360 * 2 * pi
    theta <- c(seq(0, 2 * pi, length.out = n), 0)
    
    slopes <- (-a * sin(theta) * sin(angle) + b * cos(theta) * cos(angle))/
        (-a * sin(theta) * cos(angle) - b * cos(theta) * sin(angle))
    crds <- cbind(a * cos(theta) * cos(angle) - b * sin(theta) * sin(angle) + x0,
                                a * cos(theta) * sin(angle) + b * sin(theta) * cos(angle) + y0)
    intercepts <- crds[,2] - slopes*crds[,1]
    i <- 1:(n-1)
    x <- (intercepts[i] - intercepts[i+1])/(slopes[i+1] - slopes[i])
    y <- slopes[i]*x + intercepts[i]
    outer <- cbind(c(x, x[1]),  c(y, y[1]))
    inner <- crds
    list(inner = inner, outer = outer) 
}

both <- innerouter(0,0,5, 10, 45, n=10)
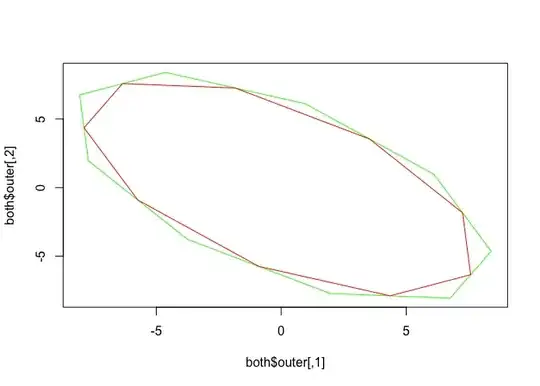
plot(both$outer, col = "green", type = "l")
lines(both$inner, col = "red")

^{Created on 2023-05-10 with reprex v2.0.2}

score 0 · Answer 2 · answered May 10 '23 at 20:02

Given a set of points that you know is a convex shape, and all the points are on the outline, then that inner polygon has lower area, as you say.

One way to generate a polygon that is larger, is to ensure that each edge of the new outer polygon touches the old polygon at those inner polygon points, ideally it should be tangential at each such point. The points of the new outer polygon would be the intersections of these tangents and lie between the points of the inner polygon.

If you can throw real surface tangents at each of the inner polygon's points then you get a perfect answer (at the polygon resolution). If you simply use the gradient between the 2 neighbour points, then you might generate edges that actually still clip the original shape, but only just.

One thought for the original problem: Could you transform one of the ellipses such that the other ellipse becomes a circle? Squashing an ellipse in any dimension simply creates a new ellipse. Does that make the problem easier to solve?

It is also worth thinking about some of the other ways of creating ellipses. An interesting one is contra-rotating circles. One circle radius max-min spins anticlockwise while orbiting clockwise at the same angular velocity centred at radius (max+min)/2. The initial starting angle defines the slope of the ellipse.

It may be that the interception points of these two ellipses can be represented as the sweep angle, allowing start and stop points for accumulating the area calculation. Dunno.

How to approximate an ellipse from the exterior?

2 Answers2