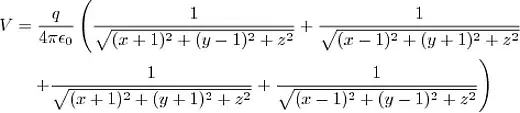How to implement weighted random selection in Google Sheets based on rarity ranking

Question

I am working on building a tool to help with my DND campaigns that will randomly give me a set number of items from the master list of the game. Needed some help wrapping my head around weighted random selection for this instance:

Column A is a list of 61 items. All of the items are assigned a rarity ranking of 1-4(1 Common, 2 Uncommon, 3 Rare, 4 Legendary), found in column B.

I need a random selection among the 61 items that is weighted according to their rarity. What also needs to be taken into consideration is that many different items share the same rarity level.

What Google Sheets formula or additional steps would I need to take? Any alternatives to reach the same result?

I've tried this formula:

=INDEX(DM_MasterList!B4:B61, MATCH(RANDBETWEEN(1, SUM(DM_MasterList!AS4:AS61)), DM_MasterList!AS4:AS61, 1))

Where B4:B61 is the item name, J4:J61 is the rarity, and AS4:AS61 is the weighted probability using the formula: 1-(B4-1)/10.

This didn't seem to work, as it was only returning the last value of the list.

please share a sample sheet with example of your data and desired result. — z'', Apr 30 '23 at 04:21
you can take a look at this: https://support.google.com/docs/thread/210153306?msgid=210182788 — z'', Apr 30 '23 at 04:47
`I need a random selection among the 61 items that is weighted according to their rarity` Would you please explain this in words of one syllable. — Tedinoz, Apr 30 '23 at 06:46
Thanks for the replies! @ztiaa that solution would work if the list of items were repetitions. The probability here would be based on the rank vs. the count of how many items are on the list. Here's that sample https://docs.google.com/spreadsheets/d/1v8iARFGS3PXNEUBG-G8T6SwgHXg51n7J9kGpOBKhy5o/edit?usp=sharing — Mitch, Apr 30 '23 at 14:42
@Tedinoz Select an item at random. Common items are chosen more often than rare items. Not one syllable but broken down at its simplest lol. — Mitch, Apr 30 '23 at 14:42

score 1 · Answer 1 · answered Apr 30 '23 at 16:18

You can assign a probability to each item based on how many times it occurs then use a Weighted Random Selection algorithm.

=ARRAYFORMULA(
   LET(count,COUNTIF(C11:C21,C11:C21),
       VLOOKUP(
         RAND(),
         HSTACK(
           SCAN(,{0;count/SUM(count)},LAMBDA(a,c,a+c)),
           B11:B21),
         2)))

And you can use the following formula to verify that the previous formula is indeed working as expected:

=ARRAYFORMULA(
   LET(q,QUERY(MAP(SEQUENCE(10000),
           LAMBDA(_,
             LET(count,COUNTIF(C11:C21,C11:C21),
                 VLOOKUP(
                   RAND(),
                   HSTACK(
                     SCAN(,{0;count/SUM(count)},LAMBDA(a,c,a+c)),
                     B11:B21),
                   2)))),
           "select Col1, count(Col1) 
            group by Col1 
            label Col1 'Item', count(Col1) 'Occurrences'"),
       IFERROR({q,INDEX(q,,2)/SUM(INDEX(q,,2))},
               "Occurrences %")))

This formula applies the algorithm 10,000 times and it shows the results.

score 0 · Accepted Answer · answered May 02 '23 at 21:22

Here is a discussion which includes a result (the Norman Gray answer) which though somewhat esoteric does seem to have a good provenance if you look back through the references. Basically you compute

-log(r)/w

where r is a random number between 0 and 1 i.e. rand() and divide it by the associated weight to get a value that you can sort on, then take the smallest n values as your sample set where n is the number of items to be selected.

Applying this to your situation would give

=ArrayFormula(ARRAY_CONSTRAIN(SORT({$B11:$B21,-LOG(RANDARRAY(11))/(1-(C11:C21-1)/10)},2,1),3,1))

This solution seems to work when I change the rarity level and assigned it a probability value instead where 1=0.7, 2=0.2, 3=0.07, 4=0.02. I changed the second to last number "3" [num_rows in the Array constraint] to 1 in order to constrain the formula to that single cell for better control of formatting. But all in all, seems to be a perfect fit. Thank you — Mitch, May 03 '23 at 23:54

How to implement weighted random selection in Google Sheets based on rarity ranking

2 Answers2