1

I am trying to calculate the MSE between two images.

  1. In Matlab the immse function contains an unexpected formula which is (norm(x(:)-y(:),2).^2)/numel(x).

  2. My teacher instead is using mean((x(:)-y(:)).^2).

I saw that the results of the method with the mean is more or less half of the other's method.

According to Wikipedia, my teacher's version seems to be the correct one.

What's the right version to use? Why are there these differences?

albertopasqualetto
  • 87
  • 1
  • 1
  • 11

1 Answers1

4

They are different forms of computing the same thing, and they do give the same answer. We can test this is the same using an example

rng(0);
x = rand(3,3); 
y = rand(3,3);
immse( x, y );       % = 0.20527
mean((x(:)-y(:)).^2) % = 0.20527

This is why...

According to the norm documentation, norm(v,2) is equivalent to norm(v) or the Euclidean norm, defined as the square root of the sum of squares

Euclidean norm

Your own Wikipedia link defines MSE as

MSE

We can combine these (using consistent lettering for n=N an k=i from the two sources)

Definition of norm(v,2) and this expression squared:

norm

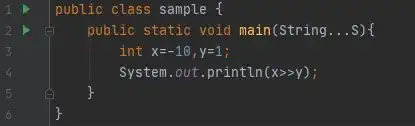
Let:

v definition

And substitute into the MSE equation:

MSE

Which is the calculation done within immse: (norm(x(:)-y(:),2).^2)/numel(x)

So the definitions given by Wikipedia and MATLAB's immse are the same. The introductory sentence for the Wiki article even mentions the norm

As it is derived from the square of Euclidean distance [...]

This is equivalent to your teacher's definition. They are using mean to perform the summation over i=1..n and division by n, and computing the square of the delta which is the same as the squared Euclidean norm.

Wolfie
  • 27,562
  • 7
  • 28
  • 55
  • 1
    Ok, thank you, I think that my problem is linked to the fact that x and y were `uint8`; if i cast them to `double`, then the value in the mean's version equals the one outputted from `imsse`. – albertopasqualetto Apr 20 '23 at 15:37