I analyse the folowing Frame using python and direct stiffness matrix method.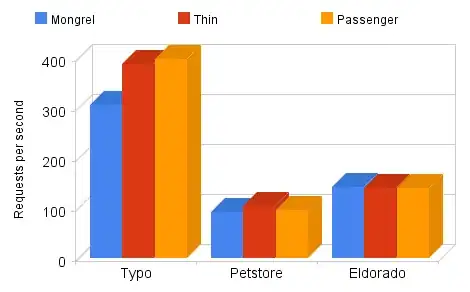
I use the following definition of coordinate system:
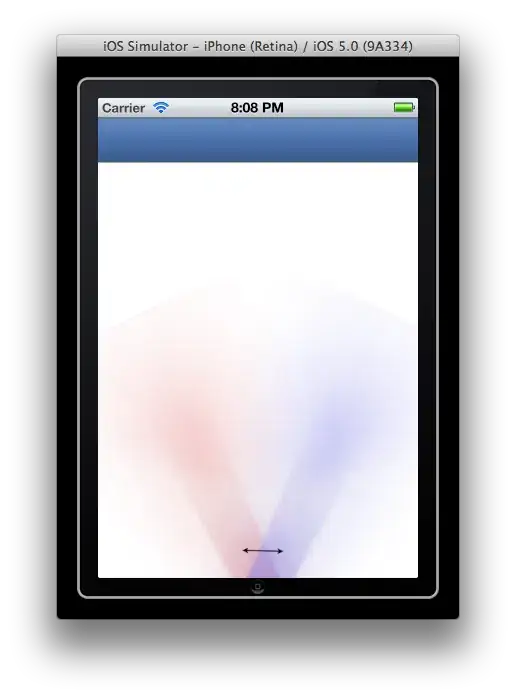
The values of displacement, which I obtain is correct, but the direction of nodal displacements in to x-direction are negative. It is not correct. I have checked the results by means of other FEM-program. The displacements in to x-direction shall be positive.
Could you please look at my code below? Maybe you will see a mistake
import numpy as np
e = 3
x_1 = 0
y_1 = 180
x_2 = 90
y_2 = 180
x_3 = 180
y_3 = 180
x_4 = 90+e
y_4 = 90
x_5 = 90
y_5 = 0
# ======================================
E_beam = 210000 # Young's modulus (MPa)
A_beam = 120 # cross-sectional area (mm^2)
I_beam = 4000 # moment of inertia (mm^4)
E_column = 210000 # Young's modulus (MPa)
A_column = 120 # cross-sectional area (mm^2)
I_column = 360 # moment of inertia (mm^4)
# ======================================
# Initialize the global stiffness matrix
N = 5 # total number of nodes
dofs_per_node = 3 # 3 degrees of freedom per node (u, v, and theta)
K_glob = np.zeros((N * dofs_per_node, N * dofs_per_node))
# ================================== element stiffness matrix 1
L_1 = np.sqrt((x_2 - x_1) ** 2 + (y_2 - y_1) ** 2) # calculate the length of the element
cos_theta_1 = (x_2 - x_1) / L_1
sin_theta_1 = (y_2 - y_1) / L_1
# Arguments in element stiffness matrix
a_1 = E_beam * A_beam / L_1
b_1 = 12 * E_beam * I_beam / L_1 ** 3
c_1 = 6 * E_beam * I_beam / L_1 ** 2
d_1 = 4 * E_beam * I_beam / L_1
e_1 = 2 * E_beam * I_beam / L_1
k_e_beam_1 = np.array([[a_1, 0, 0, -a_1, 0, 0],
[0, b_1, c_1, 0, -b_1, c_1],
[0, c_1, d_1, 0, -c_1, e_1],
[-a_1, 0, 0, a_1, 0, 0],
[0, -b_1, -c_1, 0, b_1, -c_1],
[0, c_1, e_1, 0, -c_1, d_1]])
# Compute the transformation matrix
T_beam_1 = np.array([[cos_theta_1, sin_theta_1, 0, 0, 0, 0],
[-sin_theta_1, cos_theta_1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, cos_theta_1, sin_theta_1, 0],
[0, 0, 0, -sin_theta_1, cos_theta_1, 0],
[0, 0, 0, 0, 0, 1]])
k_glob_beam_1 = np.matmul(np.matmul(T_beam_1, k_e_beam_1), np.transpose(T_beam_1))
# ================================== element stiffness matrix 2
L_2 = np.sqrt((x_3 - x_2) ** 2 + (y_3 - y_2) ** 2) # calculate the length of the element
cos_theta_2 = (x_3 - x_2) / L_2
sin_theta_2 = (y_3 - y_2) / L_2
# Arguments in element stiffness matrix
a_2 = E_beam * A_beam / L_2
b_2 = 12 * E_beam * I_beam / L_2 ** 3
c_2 = 6 * E_beam * I_beam / L_2 ** 2
d_2 = 4 * E_beam * I_beam / L_2
e_2 = 2 * E_beam * I_beam / L_2
k_e_beam_2 = np.array([[a_2, 0, 0, -a_2, 0, 0],
[0, b_2, c_2, 0, -b_2, c_2],
[0, c_2, d_2, 0, -c_2, e_2],
[-a_2, 0, 0, a_2, 0, 0],
[0, -b_2, -c_2, 0, b_2, -c_2],
[0, c_2, e_2, 0, -c_2, d_2]])
# Compute the transformation matrix
T_beam_2 = np.array([[cos_theta_2, sin_theta_2, 0, 0, 0, 0],
[-sin_theta_2, cos_theta_2, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, cos_theta_2, sin_theta_2, 0],
[0, 0, 0, -sin_theta_2, cos_theta_2, 0],
[0, 0, 0, 0, 0, 1]])
k_glob_beam_2 = np.matmul(np.matmul(T_beam_2, k_e_beam_2), np.transpose(T_beam_2))
# ================================== element stiffness matrix 3
L_3 = np.sqrt((x_4 - x_2) ** 2 + (y_4 - y_2) ** 2) # calculate the length of the element
cos_theta_3 = (x_4 - x_2) / L_3
sin_theta_3 = (y_4 - y_2) / L_3
# Arguments in element stiffness matrix
a_3 = E_column * A_column / L_3
b_3 = 12 * E_column * I_column / L_3 ** 3
c_3 = 6 * E_column * I_column / L_3 ** 2
d_3 = 4 * E_column * I_column / L_3
e_3 = 2 * E_column * I_column / L_3
k_e_column_3 = np.array([[a_3, 0, 0, -a_3, 0, 0],
[0, b_3, c_3, 0, -b_3, c_3],
[0, c_3, d_3, 0, -c_3, e_3],
[-a_3, 0, 0, a_3, 0, 0],
[0, -b_3, -c_3, 0, b_3, -c_3],
[0, c_3, e_3, 0, -c_3, d_3]])
# Compute the transformation matrix
T_column_3 = np.array([[cos_theta_3, sin_theta_3, 0, 0, 0, 0],
[-sin_theta_3, cos_theta_3, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, cos_theta_3, sin_theta_3, 0],
[0, 0, 0, -sin_theta_3, cos_theta_3, 0],
[0, 0, 0, 0, 0, 1]])
k_glob_column_3 = np.matmul(np.matmul(T_column_3, k_e_column_3), np.transpose(T_column_3))
# ================================== element stiffness matrix 4
L_4 = np.sqrt((x_5 - x_4) ** 2 + (y_5 - y_4) ** 2) # calculate the length of the element
cos_theta_4 = (x_5 - x_4) / L_4
sin_theta_4 = (y_5 - y_4) / L_4
print(cos_theta_4, sin_theta_4)
# Arguments in element stiffness matrix
a_4 = E_column * A_column / L_4
b_4 = 12 * E_column * I_column / L_4 ** 3
c_4 = 6 * E_column * I_column / L_4 ** 2
d_4 = 4 * E_column * I_column / L_4
e_4 = 2 * E_column * I_column / L_4
k_e_column_4 = np.array([[a_4, 0, 0, -a_4, 0, 0],
[0, b_4, c_4, 0, -b_4, c_4],
[0, c_4, d_4, 0, -c_4, e_4],
[-a_4, 0, 0, a_4, 0, 0],
[0, -b_4, -c_4, 0, b_4, -c_4],
[0, c_4, e_4, 0, -c_4, d_4]])
# Compute the transformation matrix
T_column_4 = np.array([[cos_theta_4, sin_theta_4, 0, 0, 0, 0],
[-sin_theta_4, cos_theta_4, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, cos_theta_4, sin_theta_4, 0],
[0, 0, 0, -sin_theta_4, cos_theta_4, 0],
[0, 0, 0, 0, 0, 1]])
k_glob_column_4 = np.matmul(np.matmul(T_column_4, k_e_column_4), np.transpose(T_column_4))
K_glob[0:6, 0:6] += k_glob_beam_1
K_glob[3:9, 3:9] += k_glob_beam_2
# ===================
K_glob[3:6, 3:6] += k_glob_column_3[0:3, 0:3]
K_glob[9:12, 3:6] += k_glob_column_3[3:6, 0:3]
K_glob[3:6, 9:12] += k_glob_column_3[0:3, 3:6]
K_glob[9:12, 9:12] += k_glob_column_3[3:6, 3:6]
K_glob[9:15, 9:15] += k_glob_column_4
# External Loads
P_0 = -10000 # (N)
# Create the zero force vector F_global
F_global = np.zeros((N * dofs_per_node, 1))
# Specify the position to add P_0 value to F_global vector
i = 4
# Add the value to x at the specified position
F_global[i, 0] += P_0
# ====================================== Applying of BC
# BC for Global stiffness matrix
K_glob_BC = K_glob
K_glob_BC = np.delete(K_glob_BC, [0, 1, 7, -2, -3], 0) # Delete rows
K_glob_BC = np.delete(K_glob_BC, [0, 1, 7, -2, -3], 1) # Delete columns
# BC for Global Force Vector
F_vec_glob_BC = F_global
F_vec_glob_BC = np.delete(F_vec_glob_BC, [0, 1, 7, -2, -3], 0) # Delete rows
# ====================================== Calculation of displacement (Linear solution)
U_glob_BC = np.matmul(np.linalg.inv(K_glob_BC), F_vec_glob_BC)
# add zero values on the position of BC
U_glob = np.insert(np.asarray(U_glob_BC), (0, 0, -1, -1, -5), values=[0], axis=0)
U_glob_resh = np.reshape(U_glob, (5, 3))
print(U_glob_resh)
Result:
[[ 0.00000000e+00 0.00000000e+00 -1.79379767e-03]
[-4.07387190e-04 -9.66284063e-02 3.66648471e-04]
[-4.07387190e-04 0.00000000e+00 1.42714920e-03]
[-4.49222495e-01 -4.83345801e-02 2.03579898e-03]
[ 0.00000000e+00 0.00000000e+00 -8.52345411e-03]]