Polars: Select first (or any) non-null column value row-wise

Question

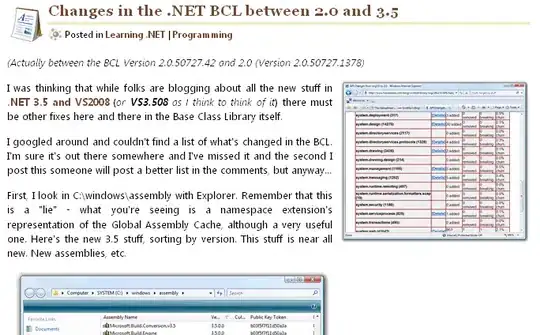
How can we select first (or any) non-null struct from polars dataframe to new column?

Input data:

structs_a = [
    {"a_key_1": 1, "a_key_2": "a" },
    {"a_key_1": None, "a_key_2": None }
]
structs_b = [
    {"b_key_1": None, "b_key_2": None },
    {"b_key_1": "b", "b_key_2": 2 }
]
df = pl.DataFrame([structs_a, structs_b])
df

┌─────────────┬─────────────┐
│ column_0    ┆ column_1    │
│ ---         ┆ ---         │
│ struct[2]   ┆ struct[2]   │
╞═════════════╪═════════════╡
│ {1,"a"}     ┆ {null,null} │
│ {null,null} ┆ {"b",2}     │
└─────────────┴─────────────┘

What I've tried so far: Concatenating values to list and dropping nulls, but for reasons I yet have to understand this results in empty list of struct**[4]**

df.with_columns(
             pl.concat_list([
                 "column_0",
                 "column_1",
             ]).arr.eval(pl.element().drop_nulls()).alias('final_column'))

My result:

┌─────────────┬─────────────┬─────────────────┐
│ column_0    ┆ column_1    ┆ final_column    │
│ ---         ┆ ---         ┆ ---             │
│ struct[2]   ┆ struct[2]   ┆ list[struct[4]] │
╞═════════════╪═════════════╪═════════════════╡
│ {1,"a"}     ┆ {null,null} ┆ []              │
│ {null,null} ┆ {"b",2}     ┆ []              │
└─────────────┴─────────────┴─────────────────┘

Desirable result:

┌─────────────┬─────────────┬─────────────────┐
│ column_0    ┆ column_1    ┆ final_column    │
│ ---         ┆ ---         ┆ ---             │
│ struct[2]   ┆ struct[2]   ┆ struct[2]       │
╞═════════════╪═════════════╪═════════════════╡
│ {1,"a"}     ┆ {null,null} ┆ {1,"a"}         │ <- Non-null value from column_0
│ {null,null} ┆ {"b",2}     ┆ {"b",2}         │ <- Non-null value from column_1
└─────────────┴─────────────┴─────────────────┘

UPD: Probably should experiment with coalesce but direct implementation did not result as desired:

df.with_columns(
             pl.coalesce([
                 "column_0",
                 "column_1",
             ]).alias('final_column'))

one more undesired result:

┌─────────────┬─────────────┬───────────────────────┐
│ column_0    ┆ column_1    ┆ final_column          │
│ ---         ┆ ---         ┆ ---                   │
│ struct[2]   ┆ struct[2]   ┆ struct[4]             │
╞═════════════╪═════════════╪═══════════════════════╡
│ {1,"a"}     ┆ {null,null} ┆ {null,null,null,null} │
│ {null,null} ┆ {"b",2}     ┆ {null,null,"b",2}     │
└─────────────┴─────────────┴───────────────────────┘

The lists are empty, because every strut then includes a null: `df.select([pl.concat_list(pl.all()).alias("final_column")])` returns ```┌─────────────────────────────────────┐ │ final_column │ │ --- │ │ list[struct[4]] │ ╞═════════════════════════════════════╡ │ [{1,"a",null,null}, {null,null,n... │ │ [{null,null,null,null}, {null,nu... │ └─────────────────────────────────────┘ ``` — DobbyTheElf, Mar 15 '23 at 10:09
If you check `.arr.eval(pl.element().is_null())` it does seem to know what should be dropped. It seems like something is not "struct aware". The `.coalesce` works if they are non-struct columns. — jqurious, Mar 15 '23 at 11:41

mrCatlost · Answer 1 · 2023-04-11T13:50:53.123

Introduction

This question so concerning to dictionaries. I have been testing different ways to create a solution for your question, i got a fast solution that works well where i get the result you are searching for.

If you want to filter by null values, as you are using dictionaries you have to go deep into the keys and values of that dictionaries because if you are checking for nulls or nas values you´ll check the rows values.

First approach

A way that is going to works for sure is to iterate the dataframe and check the values inside of it, you can do it in some different ways i used shape function.

new_column = [] #Define the array variable

for i in range(df.shape[0]): #iterate over rows
    for j in range(df.shape[1]): #iterate over columns
        value = df.at[i, j] # get cell value
        values = value.values() # get the values from the cell value (Inside dictionary value)
        if not None in values: # check if there is some None values in the cell
            new_column.append(value) #Add the cell value into the array
      
df['final_column'] = new_column #Create the new column using the array with new values

OUTPUT:

    0   1   final_column
0   {'a_key_1': 1, 'a_key_2': 'a'}  {'a_key_1': None, 'a_key_2': None}  {'a_key_1': 1, 'a_key_2': 'a'}
1   {'b_key_1': None, 'b_key_2': None}  {'b_key_1': 'b', 'b_key_2': 2}  {'b_key_1': 'b', 'b_key_2': 2}

Second approach

Iterate by the DF in a different way

new_column = [] #Define the array variable

for rowIndex, row in df.iterrows(): #iterate over rows
    for columnIndex, value in row.items(): # iterate over columns
        values = value.values() # get the values from the cells
        if not None in values: # check if there is some None values in the cell
            new_column.append(value) #Add the cell value into the array
      
df6['final_column'] = new_column #Create the new column using the array with new values

This method give the same corret result.

Thanks a lot for your solution and efforts! It definitely works, but due to dataset size and implementation approach I'm still looking for a polars-based solution — Krank, Mar 15 '23 at 10:15
Good to know, i´ll check and if i can give a polars-based solution i´ll post it. Good luck anyway! — mrCatlost, Mar 15 '23 at 10:29

jqurious · Answer 2 · 2023-04-11T15:57:31.323

Update: Perhaps you could .unnest() the structs:

df.with_columns(
   df.unnest(df.columns)
     .select(
        pl.concat_list(pl.all())
          .arr.eval(pl.element().drop_nulls(), parallel=True)
          .arr.to_struct())
)

shape: (2, 3)
┌─────────────┬─────────────┬───────────┐
│ column_0    ┆ column_1    ┆ a_key_1   │
│ ---         ┆ ---         ┆ ---       │
│ struct[2]   ┆ struct[2]   ┆ struct[2] │
╞═════════════╪═════════════╪═══════════╡
│ {1,"a"}     ┆ {null,null} ┆ {"1","a"} │
│ {null,null} ┆ {"b",2}     ┆ {"b","2"} │
└─────────────┴─────────────┴───────────┘

This is not an answer, but to address the empty struct issue as it confused me:

When the keys of each struct are the same - the result of .concat_list is as one would expect:

structs_a = [ {"a_key_1": 1, "a_key_2": "a" }, ]
structs_b = [ {"a_key_1": None, "a_key_2": None }, ]

df = pl.DataFrame([structs_a, structs_b])

df.select(pl.concat_list(pl.all()))

shape: (1, 1)
┌────────────────────────┐
│ column_0               │
│ ---                    │
│ list[struct[2]]        │
╞════════════════════════╡
│ [{1,"a"}, {null,null}] │
└────────────────────────┘

When the keys differ:

structs_a = [ {"a_key_1": 1, "a_key_2": "a" }, ]
structs_b = [ {"b_key_1": None, "b_key_2": None }, ]

df = pl.DataFrame([structs_a, structs_b])

df.select(pl.concat_list(pl.all()))

shape: (1, 1)
┌─────────────────────────────────────┐
│ column_0                            │
│ ---                                 │
│ list[struct[4]]                     │
╞═════════════════════════════════════╡
│ [{1,"a",null,null}, {null,null,n... │
└─────────────────────────────────────┘

It looks like the union of all the keys is used - but you don't notice that when all the keys are the same.

It may be easier to see if everything is unnested:

same keys:

df.select(pl.concat_list(pl.all())).explode(pl.all()).unnest("column_0")

shape: (2, 2)
┌─────────┬─────────┐
│ a_key_1 | a_key_2 │
│ ---     | ---     │
│ i64     | str     │
╞═════════╪═════════╡
│ 1       | a       │
│ null    | null    │
└─────────┴─────────┘

different keys:

df.select(pl.concat_list(pl.all())).explode(pl.all()).unnest("column_0")

shape: (2, 4)
┌─────────┬─────────┬─────────┬─────────┐
│ a_key_1 | a_key_2 | b_key_1 | b_key_2 │
│ ---     | ---     | ---     | ---     │
│ i64     | str     | i32     | i32     │
╞═════════╪═════════╪═════════╪═════════╡
│ 1       | a       | null    | null    │
│ null    | null    | null    | null    │
└─────────┴─────────┴─────────┴─────────┘

Polars: Select first (or any) non-null column value row-wise

2 Answers2

Introduction

First approach

OUTPUT:

Second approach