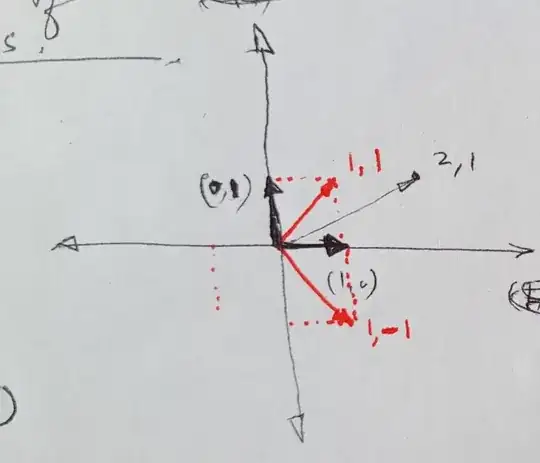
In mathematics, let’s assume the original basis is [1 0] and [0 1].
We can write [1 1] as a linear combination of the original basis.
 Where:
Where: 
We can write [1 -1] as a linear combination of the original basis.
 Where:
Where:
Further let’s assume [1 1] and [1 -1] is the new basis.
We can write any vector let’s say [2 1] as a linear combination of the new basis.
 Where :
Where : 
Also acknowledging that [ 2 1] can also be written in the original basis as  Where :
Where : 
In effect, every vector can be written as a linear combination of any 2 vectors.
Extending the same discussion to the complex plane, and treating the 90° line as the imaginary axis/dimension,

2+3j can be written as the linear combination of 2 basis vectors (1+0j) and (0+1j) as
2+3j = x(1+0j) + y(0+1j)
Where x=2 and y=3
We make a special note here that in the case of the complex plane, x and y are real, whereas the basis vectors are complex numbers.
NOW, if we extend the same discussion to Quantum Computing to describe the state of a qubit, we describe the state of 1 qubit as -
|q⟩ = α|0⟩ + β|1⟩
Where |0⟩ and |1⟩ can be explained according to another accept answer on Stack exchange for a different question. The numbers in notations like |n⟩ are the analogues of indices in matrix notation. That is, |0⟩=e0, |1⟩=e1, etc., where en is the vector which has a 1 in the nth position and 0 in the other entries. For qubits in quantum computers, the dimension is 2, so we have |0⟩=e0=(1,0) and |1⟩=e1=(0,1).
Accordingly - I am assuming –
|0⟩= e0 = (1,0) = (Yes_it_is_Zero, No_it_is_not_1)
and
|1⟩= e1 = (0,1) = (No_it_is_not_Zero, Yes_it_is_1)
This also means that |0⟩ and |1⟩ themselves are not complex unless each of them are represented as a superposition of |0⟩ and |1⟩ with α and β.
Question 1: So, if |0⟩ and |1⟩ themselves are not complex, then, why do we need x and y, i.e. α and β to be complex here? This is different from the note earlier for the complex plane, where the basis was complex and the x,y were real numbers. What is the need for probability amplitudes to be complex numbers? What is the intuition behind probability amplitudes α and β to be complex numbers?
Question 2: What is the intuition behind probability amplitudes being squared to find probabilities of |0⟩ state (with α^2 ) or |1⟩ state (with β^2 ).
Question 3: And what is the meaning of pure states versus mixed states in my current framework of understanding?
Edit: I thought it would be nice to post it on the StackExchange Mathematics site too