When using skolemization to replace existentially quantified variables in an expression, any existential bound at the top level can be replaced by a new globally unique constant, however if the existential is under a universal quantification it cannot be replaced by a constant. It must be replaced instead by a new globally unique predicate symbol which is applied to all the universally quantified variables in scope.
I don't understand why this must be so, since the uniqueness of the new predicate symbol must surely prevent it from unifying with any other object but itself.
 , where
, where  is logically stronger, as
is logically stronger, as 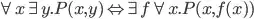 , and that
, and that 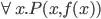 is satisfiable iff
is satisfiable iff 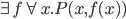 is. Your suggestion breaks down because
is. Your suggestion breaks down because 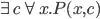 is not equivalent to
is not equivalent to 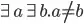 , and
, and