Python Numpy polyfit gets the same as Excel Linear for slope

Question

By the use of below, I get the slope of a list of number.

It's referenced from the answer to this question, Finding increasing trend in Pandas.

import numpy as np
import pandas as pd

def trendline(data, order=1):
    coeffs = np.polyfit(data.index.values, list(data), order)
    slope = coeffs[-2]
    return float(slope)

score = [275,1625,7202,6653,1000,2287,3824,3812,2152,4108,255,2402]

df = pd.DataFrame({'Score': score})

slope = trendline(df['Score'])

print(slope)

# -80.84965034965013

When in Excel, the slope is about the same when the trendline was plot by Liner method. The slope is different when Excel plot it using the Polynomial.

The Python function "trendline" seems defined by "np.polyfit". Why it can calculate the same as Excel does it in Liner?

(if I applied or worked it wrongly somewhere?)

Answer 1

Because in the function trendline, the default order is 1 which corresponds to the argument deg in the function np.polyfit. The deg is the Degree of the fitting polynomial, when order=1, that means you are using a linear fit.

Here we add a function to show the result with different orders:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def trendline(data, order=2):
    coeffs = np.polyfit(data.index.values, list(data), order)
    # slope = coeffs[-2]
    return coeffs

def get_smooth(x, coeffs):
    y = 0
    for exp, coef in enumerate(coeffs):
        y_temp = coef * x**(len(coeffs)-exp-1)
        y = y + y_temp
    return y

score = [275,1625,7202,6653,1000,2287,3824,3812,2152,4108,255,2402]

x = np.arange(len(score))
x_new = np.linspace(0, len(score)-1, 50)

df = pd.DataFrame({'Score': score})

coeffs1 = trendline(df['Score'], order=1)

y1 = get_smooth(x_new, coeffs1)

plt.figure()
plt.plot(x, score)
plt.plot(x_new, y1, '.')
plt.title("Polyfit with order=1")

coeffs2 = trendline(df['Score'], order=2)

y2 = get_smooth(x_new, coeffs2)

plt.figure()
plt.plot(x, score)
plt.plot(x_new, y2, '.')
plt.title("Polyfit with order=2")

We get two figures :

Polyfit with an order 1 :

Polyfit with an order 2 :

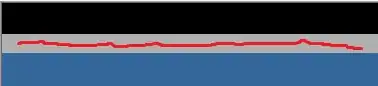
The second figure is when you use Polynomial in Excel.

Update

For showing the equation, I borrowed an answer from : How to derive equation from Numpy's polyfit?

Full codes :

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sympy import S, symbols, printing

def trendline(data, order=2):
    coeffs = np.polyfit(data.index.values, list(data), order)
    # slope = coeffs[-2]
    return coeffs

def get_smooth(x, coeffs):
    y = 0
    for exp, coef in enumerate(coeffs):
        y_temp = coef * x**(len(coeffs)-exp-1)
        y = y + y_temp
    return y


def generate_label(coeffs):
    x = symbols("x")
    poly = sum(S("{:6.5f}".format(v))*x**i for i, v in enumerate(coeffs[::-1]))
    eq_latex = printing.latex(poly)
    return eq_latex

score = [275,1625,7202,6653,1000,2287,3824,3812,2152,4108,255,2402]

x = np.arange(len(score))
x_new = np.linspace(0, len(score)-1, 50)

df = pd.DataFrame({'Score': score})

coeffs2 = trendline(df['Score'], order=2)

y2 = get_smooth(x_new, coeffs2)
eq_latex_2 = generate_label(coeffs2)

plt.figure()
plt.plot(x, score)
plt.plot(x_new, y2, '.', label="${}$".format(eq_latex_2))
plt.title("Polyfit with order=2")
plt.legend(fontsize="small")

Then the figure :