-1

I'm trying to solve the following nonlinear system of equations with $sigma^2_2$ and $\mu_2$ unknown : 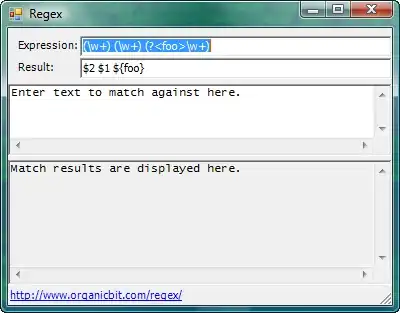enter image description here And here is the code I used in R with the rootSolve library :

library(rootSolve)
mu_1 <- -2.931476
sigmasq_1 <- (1.084857)^2
mu_Z <- -6.717234
sigmasq_Z <- 0.104320

model <- function(x) c(F1 = log(((exp(2*mu_1+sigmasq_1)*(exp(sigmasq_1)-1))+(exp(2*x[1]+x[2])*(exp(x[2])-1)))/
                                 ((exp(mu_1+sigmasq_1/2)+exp(x[1]+x[2]/2))^2)+1)-sigmasq_Z, 
                       F2 = log(exp(mu_1+sigmasq_1/2)+exp(x[1]+x[2]/2))-sigmasq_Z/2-mu_Z)
(ss <- multiroot(f = model, start = c(1.5, 0)))

However this gives absurd result and the following warning :

Warning messages: 1: In stode(y, times, func, parms = parms, ...) : error during factorisation of matrix (dgefa); singular matrix 2: In stode(y, times, func, parms = parms, ...) : steady-state not reached

outofthegreen
  • 352
  • 1
  • 13

1 Answers1

0

The system has an explicit solution.

From the second equation, the argument of the logarithm is a known value, and it can be substituted in the first equation, at the denominator. It also gives us the value of exp(µ2 + σ2²/2), the square of which which we can substitute in the first equation. Finally the first equation can be written exp(σ2²)-1=a, which is pretty easy.