0

so I've been trying to plot this surface, that is parametrized in disk-cyclide coordinates:

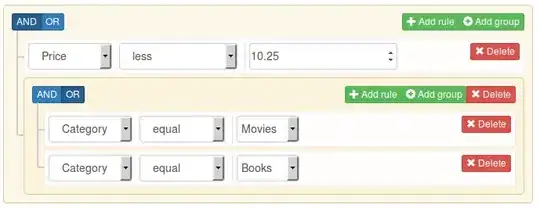
parametric functions

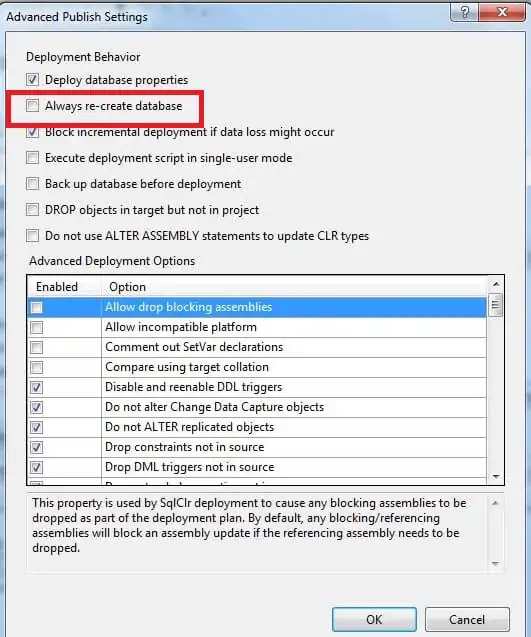
Lambda function

But I've been getting an error saying that Z must be 2 dimensional. How can I make it that way while it is parametrized by 3 variables?

Using this code:

size = 250    
psi = np.linspace(0, 2*np.pi, size)
mu = np.linspace(0,K, size)
nu =  np.linspace(0, Kl, size)
Mu, Nu, Psi = np.meshgrid(mu, nu, psi)

k = 0.963
kl = 0.270

K = sp.special.ellipk(k)

Kl = sp.special.ellipk(kl)


Lambda = 1 - (sp.special.ellipj(Mu,k)[2]**2)*(sp.special.ellipj(Nu,kl)[0])

x = (1/Lambda)*(sp.special.ellipj(Mu,k)[1])*(sp.special.ellipj(Nu,kl)[1])*np.cos(Psi)

y = (a/Lambda)*(sp.special.ellipj(Mu,k)[1])*(sp.special.ellipj(Nu,kl)[1])*np.sin(Psi)

z = (a/Lambda)*(sp.special.ellipj(Mu,k)[0])*(sp.special.ellipj(Mu,k)[2])*(sp.special.ellipj(Nu,kl)[0])*(sp.special.ellipj(Nu,kl)[2])

fig = plt.figure()
ax = fig.gca(projection = '3d')

ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap="hot")
plt.show()
JohanC
  • 71,591
  • 8
  • 33
  • 66
João Renato
  • 1
  • 1
  • `plot_surface` needs `z` to be defined on a grid-like structure (an X and a Y direction) stored in a 2D array. If you just have unorganized x, y and z values, you can use `ax.trisurf(x, y, z, cmap='hot')` instead. See e.g. [how to use plot_trisurf](https://stackoverflow.com/questions/44244297/how-to-use-plot-trisurf) – JohanC Feb 01 '23 at 17:55
  • As your x, y and z seem to be 3D, you might need to "ravel" them to long 1D arrays. And you might want to set `size` to something smaller, e.g. 50 and then call `ax.plot_trisurf(x.ravel(), y.ravel(), z.ravel(), cmap="hot")`. – JohanC Feb 01 '23 at 18:09

0 Answers0