Extrude a concave, complex polygon in PyVista

Question

I wish to take a concave and complex (containing holes) polygon and extrude it 'vertically' into a polyhedron, purely for visualisation. I begin with a shapely Polygon, like below:

poly = Polygon(
    [(0,0), (10,0), (10,10), (5,8), (0,10), (1,7), (0,5), (1,3)], 
    holes=[
        [(2,2),(4,2),(4,4),(2,4)],
        [(6,6), (7,6), (6.5,6.5), (7,7), (6,7), (6.2,6.5)]])

which I correctly plot (reorientating the exterior coordinates to be clockwise, and the hole coordinates to be counterclockwise) in matplotlib as:

I then seek to render this polygon extruded out-of-the-page (along z), using PyVista. There are a few hurdles; PyVista doesn't directly support concave (nor complex) input to its PolyData type. So we first create an extrusion of simple (hole-free) concave polygons, as per this discussion.

def extrude_simple_polygon(xy, z0, z1):

    # force counter-clockwise ordering, so PyVista interprets polygon correctly
    xy = _reorient_coords(xy, clockwise=False)

    # remove duplication of first & last vertex
    xyz0 = [(x,y,z0) for x,y in xy]
    if (xyz0[0] == xyz0[-1]):
        xyz0.pop()

    # explicitly set edge_source
    base_vert = [len(xyz0)] + list(range(len(xyz0)))
    base_data = pyvista.PolyData(xyz0, base_vert)
    base_mesh = base_data.delaunay_2d(edge_source=base_data)
    vol_mesh  = base_mesh.extrude((0, 0, z1-z0), capping=True)

    # force triangulation, so PyVista allows boolean_difference
    return vol_mesh.triangulate()

Observe this works when extruding the outer polygon and each of its internal polygons in-turn:

extrude_simple_polygon(list(poly.exterior.coords), 0, 5).plot()

extrude_simple_polygon(list(poly.interiors[0].coords), 0, 5).plot()
extrude_simple_polygon(list(poly.interiors[1].coords), 0, 5).plot()

I reasoned that to create an extrusion of the original complex polygon, I could compute the boolean_difference. Alas, the result of

outer_vol = extrude_simple_polygon(list(poly.exterior.coords), 0, 5)
for hole in poly.interiors:
    hole_vol = extrude_simple_polygon(list(hole.coords), 0, 5)
    outer_vol = outer_vol.boolean_difference(hole_vol)

outer_vol.plot()

is erroneous:

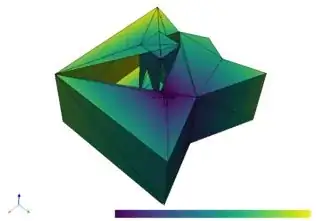
The doc advises to inspect the normals via plot_normals, revealing that all extruded volumes have inward-pointing (or else, unexpected) normals:

The extrude doc mentions nothing of the extruded surface normals nor the original object (in this case, a polygon) orientation.

We could be forgiven for expecting our polygons must be clockwise, so we set clockwise=True in the first line of extrude_simple_polygon and try again. Alas, PolyData now misinterprets our base polygon; calling base_mesh.plot() reveals (what should look like our original blue outer polygon):

with extrusion

• Does PyVista always expect counter-clockwise polygons?
• Why does extrude create volumes with inward-pointing surface normals?
• How can I correct the extruded surface normals?
• Otherwise, how can I make PyVista correctly visualise what should be an incredibly simply-extruded concave complex polygon??

Answer 1

You're very close. What you have to do is use a single call to delaunay_2d() with all three polygons (i.e., the enclosing one and the two holes) as edge source (loop source?). It's also important to have faces (rather than lines) from each polygon; this is what makes it possible to enforce the holeyness of the holes.

Here's a complete example for your input (where I manually flipped the orientation of the holes; you seem to have a _reorient_coords() helper that you should use instead):

import pyvista as pv

# coordinates of enclosing polygon
poly_points = [
    (0, 0), (10, 0), (10, 10), (5, 8), (0, 10), (1, 7), (0, 5), (1, 3),
]
# hole point order hard-coded here; use your _reorient_coords() function
holes = [
    [(2, 2), (4, 2), (4, 4), (2, 4)][::-1],
    [(6, 6), (7, 6), (6.5, 6.5), (7, 7), (6, 7), (6.2, 6.5)][::-1],
]

z0, z1 = 0.0, 5.0

def points_2d_to_poly(points, z):
    """Convert a sequence of 2d coordinates to a polydata with a polygon."""
    faces = [len(points), *range(len(points))]
    poly = pv.PolyData([p + (z,) for p in points], faces=faces)
    return poly

# bounding polygon
polygon = points_2d_to_poly(poly_points, z0)

# add all holes
for hole_points in holes:
    polygon += points_2d_to_poly(hole_points, z0)

# triangulate poly with all three subpolygons supplying edges
# (relative face orientation is critical here)
polygon_with_holes = polygon.delaunay_2d(edge_source=polygon)

# extrude
holey_solid = polygon_with_holes.extrude((0, 0, z1 - z0), capping=True)
holey_solid.plot()

Here's the top view of the polygon pre-extrusion:

plotter = pv.Plotter()
plotter.add_mesh(polygon_with_holes, show_edges=True, color='cyan')
plotter.view_xy()
plotter.show()