How to translate game state for a game turn into a limited set of moves?

Question

I'm having a very difficult time determining how to translate a game state for a specific turn in a game I'm developing into a limited sequence of moves that represents the moves taken for that turn. I'd appreciate advice on how I can do this.

NOTE: the game is now live! And if anyone wants to try it, it's at: https://mystikaze.com
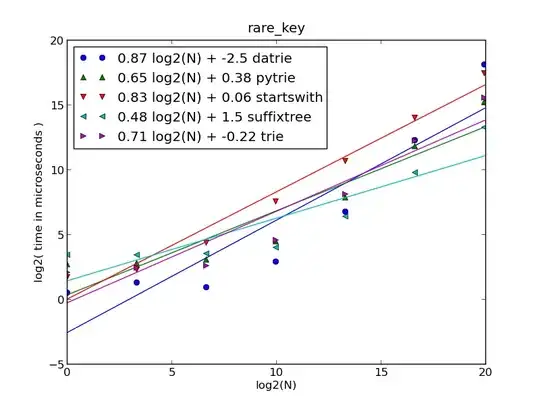
(I ended up implementing an algorithm for storing game moves that may not be fully efficient but I think does guarantee that the move list for any given turn cannot be unbounded/infinitely long).

The rules for the game are relatively simple. There's a hex board, with hexes belonging to 2 players. On any given turn, pieces can already exist on the board, having been purchased on a previous turn, or they can be purchased onto the board (a yellow piece represents its being purchased onto the board this turn).

These pieces are "active", and can still be moved. Pieces can also be combined, and will still remain "active". They can be combined either by moving an existing piece onto another piece, or by purchasing a new piece onto an existing piece. When combined, an upgraded piece will exist on the target hex. Pieces can be of 3 strengths; X, Y, and Z. X combining with X gives Y, and X with Y gives Z.

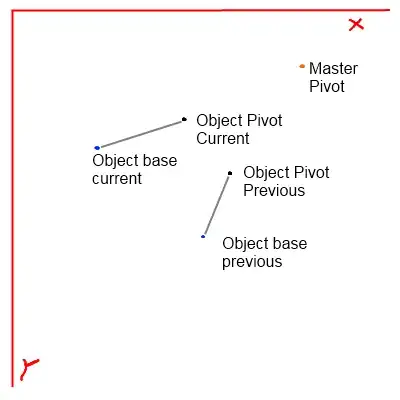
Pieces can continue to be merged like this and remain "active". A piece can be moved to another hex in its own territory and remain "active". A piece stops being "active" when it is moved to capture the other player's hex. It cannot move after that, although it can still be combined with. Green below indicates an inactive piece.

A piece can also be summoned directly on top of another piece, resulting in an upgraded piece (if it was already active, it stays active; if it was inactive, it stays inactive):

Now, this is pretty easy to represent in game state; just update the state of the pieces and the board to reflect whatever's currently true. And it's quite easy to convert it into a sequence of moves as long as you theoretically allow for that sequence of moves to be unbounded; pieces could remain active and move to and fro ad infinitum. Of course, I want to keep the sequence of moves limited. This is where I'm having trouble. I have the following 2 moves:

• Move piece to location
• Summon piece to location

How can I convert the moves a player makes into a limited sequence of moves to represent what the player actually did, leading to the final state? I don't know if I'm missing something, but this seems to get almost impossibly complex to figure out. If you have pieces moving around within their own territory and remaining active, you might think you could just update the move in-place to the new coordinates instead of adding a new move to the new coordinates, but what if there is another move where a piece combines with that piece to form an upgraded piece, which relied upon the first piece moving to its first set of coordinates? Updating the move coordinates in-place now means that that second combination move becomes a regular move because it is now moving onto an empty hex, yet it should remain a combination move (the board state will in fact be the combined piece having moved to the new coordinates).

Conceptually, there should always be a limited sequence of moves that can represent any operation. However I am finding it extremely hard to figure out how to write an algorithm to do this automatically. I think an algorithm that would at least prevent the unbounded nature of the moves would be to say "a piece's most recent move is updated instead of adding the new move to the list if that most recent move is not a combine or capture operation". That should always result in the game state being correctly created by the move set, and prevent unlimited cycles. However that could still result in quite a lot of moves. For instance if you had 10 pieces in a territory, you could move all 1, capture with 1, move the remaining 9, combine one with another, move the remaining 8, etc. potentially resulting in over 60 moves from 10 pieces. It would be nice if there were an algorithm to get this down a bit, and I'm still not 100% sure that even this algorithm doesn't have some edge cases where it wouldn't work.

Am I missing a relatively straightforward way to solve this problem? The rules must stay the same but I'm open to suggestions about perhaps introducing new move types if that would help solve the problem, too.

Answer 1

From what I understand from your question and the comments, the problem seems to be the large amount of possible moves to be made in a single turn, including combinations. I couldn't think of a complete algorithm, but I think I can give you a pretty good starting point. In the end of the answer you will find the edge cases not contemplated here and possible solutions to them.

---

My suggestion is not to think in terms of movements, but in terms of events, and to check that each event is possible, according to the rules.

Previous assumptions and definitions.

• The size of the board, the number of pieces and the number of purchasable pieces are finite.

• Each piece is labelled with an ID of the form T_s, where T is the piece type (X, Y, Z) and s is a counter (1, 2, 3, 4...).

• You have access to the information from the game state before the game turn and after it.

• You can only purchase pieces of type X.

• Possible events:

  • Piece moved
  • Piece purchased

• No event of combination because it can always be translated to one or more events of movement. In other words: we can assume that if a piece is moved after being combined with another, there is an equivalent sequence of movements where both pieces just move to the final destination and get combined there. X_1 -> X_2 = Y_1; Y_1 -> NEWCELL equals to X_1 -> NEWCELL; X_2 -> NEWCELL

The algorithm

1. My algorithm is based on the fact that you can represent the game state as disjoint sets of labelled pieces. So the first thing to do is to use an inundation algorithm to compute the disjoint areas (area = set of cells) of the board in the initial state that belong to the player. Let's call these areas A_1, A_2, etc. It is not necessary to have this representation for the final state.

2. You also need to compute the difference of the initial pieces set and the final one, to determine the number of combinations and purchases made.

   • A. Let's call N_T_s to the number of pieces of type T in the starting state and N_T_f to the number of pieces of type T in the final state. You can calculate the number of purchased pieces like this: (N_X_f + 2*N_Y_f + 3*N_Z_f) - (N_X_s + 2*N_Y_s + 3*N_Z_s).
   • B. As the pieces are labelled, you can build a set NEW of pieces that were not present in the initial state. We will assume these are either the result of a purchase or a combination.

3. Prepare some variables:

   • Set a counter of PURCHASED with the initial value computed in the step 2A.

   For each area A_i

   • Create a set of COMBINED_i with the pieces from A_i that are not present in the final state (as the only way for a piece to disappear is to be combined).
   • Define an area M_i as the union of A_i and all its adjacent cells.

4. For each area A_i and for each piece inside it:

   • A. If the piece is not inside NEW: its final position must be inside M_i. Given that a deactivated cell cannot move, it shouldn't move any further.

5. For each piece inside NEW: The piece must be inside one of the M_i areas (otherwise the turn is invalid). Let's call it M_p.

   • A. If the piece is of type X: decrease the value of the counter PURCHASED. If the value is negative, the turn is not valid.

   • B. If the piece is of type Y:

     • If there exist two pieces X inside COMBINED_p, remove them from the set.
     • Else, if there exists a single X inside COMBINED_p remove it from the set and decrease the value of the counter PURCHASED.
     • Else, decrease twice the value of the counter PURCHASED.

   • C. If the piece is of type Z:

     • If there exist an X and a Y inside COMBINED_p, remove them from the set.
     • Else, if there exists an Y but no X inside COMBINED_p remove it from the set and decrease the value of the counter PURCHASED.
     • Else if there exist two X inside COMBINED_p remove them from the set and decrease the value of the counter PURCHASED.
     • Else if there exists a single X inside COMBINED_p remove it from the set and decrease twice the value of the counter PURCHASED.
     • Else, decrease thrice the value of the counter PURCHASED.

How to store events

• In step 4A you can store the movement of the piece.
• In step 5A you can store the purchase of the piece.
• In steps 5B and 5C you can store the movements of the pieces you remove from the COMBINED_p (movement from their initial position to the position of the final combined piece) sets and the purchase of pieces each time you decrease the counter.

Observations

• I didn't mention it but I guess you should remove from the areas M_i all the cells occupied by enemy pieces.
• The order of if-elses in step 5 is very important. It is the greedy approach to the Change-making problem. Keep it in mind in case you added more combinations to the game.
• You haven't told us where the currency for purchasing pieces comes from, but you can quickly check the validity of the purchases made in step 2A.
• In case that the board was not finite (maybe it is automatically generated), then you could apply this algorithm to the finite surface defined by the presence of the pieces in both states.

Edge cases

1. The disjoint areas might not represent the true space where a piece can move, given that pieces are solid and can't be trespassed by other pieces without combining.

   For example: I have an area that is just a row like this: #XY##. My algorithm would approve a final state ##YX#. A possible approach would be to check the existence of disjoint sub-areas and treat them separately.

2. In the final state, two initially disjoint areas could become joined thanks to a piece (let's call it a bridge) that moves into an intermediate cell that is adjacent to both areas at the same time. Precisely thanks to the first edge case, we don't need to worry about other existing pieces moving from one area to another through the bridge... but if we find that the bridge is a recently combined piece (in other words, it belongs to NEW), then we have to make extra checks and even backtracking to determine where did the combined pieces came from, because we can no longer assume they came from a single area plus possible purchases.

---

As you see, this is not a complete algorithm, but it may settle some working ground. The main contribution I attempt to make is the approach of the disjoint areas and the event focused analysis. If you want, I could try to elaborate further on the edge cases and try to find solutions and incorporate them in the whole algorithm.

Answer 2

In the end, given the flexibility of the ruleset, I had to come up with a different algorithm from the ones suggested. I came at the problem from the other end; instead of considering how to absolutely minimize the number of moves, what is it that allows the unbounded potential for number of moves? It's the fact that active pieces can move an unbounded number of times between empty hexes. Everything else is bounded quite nicely; a piece can move, then combine, but that's it; the combination removes it from the board and upgrades the underlying piece. It can move, then capture, but that ends its turn. So, to eliminate the unbounded nature of the moves list, I ended up with the following algorithm for validating a moves list:

• Only one summon operation for a piece is allowed
• For a move operation, any moves for a piece after it has captured are forbidden
• Multiple non-combine/non-capture moves in a row for a piece are forbidden, if there are no moves between that piece's two moves that are combine/capture moves
• When a piece is combined, it is removed from the board and the underlying piece is upgraded, meaning that that piece then can't move after the combine operation as it no longer exists on the board

This does mean that you can get a piece moving before a combine or capture operation, and a piece can even have multiple non-combine/non-capture moves in a turn if they are separated by other pieces being combined - which I think is somewhat necessary in case another piece is then moved on top of it for combination - but multiple such moves in a row are illegal, nicely limiting the bounds of how many moves may be submitted for a turn.

On the client side, it detects if a piece move is the piece moving twice in a row within its own territory. If it isn't, it just adds the move. If it is, it checks whether there is a move since the existing one with the same target coords. If there isn't, it just updates the existing move in-place. If there is, it splices that move out as well as the existing move for this piece, and inserts it at the end of the moves list, followed by this piece's move; this is needed to reflect the fact that this piece is now being combined with that piece, in the correct order.

This seems to work, but it's rather complicated and confusing. Seems to be the nature of the problem, though!

Answer 3

This is actually similar task as i.e. find what moves you need to do in chess to change from one state to another. It can even happen that the solution does not exist.

By default its O(x^n) issue, where x is possible moves and n number of moves. Yes, its growing quite rapidly. In general you have to check all possible moves in BFS way each turn until you find the solution.

Actually if you are successful with it, you are very close to implementing AI, you just add some scores to your moves and thats it.

To optimize it, you can use some heuristics (to i.e. prefer movement in correct direction or not expanding branches that does not make sense - i.e. when piece get combined and you know it is not possible). However there can be situations it will not be sufficient (i.e. piece needs to travel really far away around some enemy position to not be catched).

To get you further - google how to create AI for five-in-a-row or chess, your task will be very similar. Unless you want to create AI, I would strongly recommend to get all movements from client - even if you make a bit more movements than necessary.