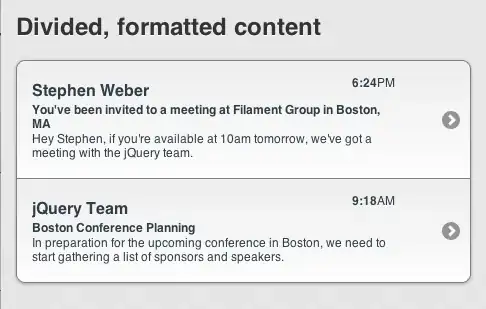
In Voronoi tiling there is a 1:1 correspondence between the points and the tiles, so one can easily map a fill aesthetic to the tiles. Each row in your data frame will have its own tile and therefore can specify a fill, an alpha, etc.
This is not the case in Delaunay tiling, where each row in your data frame describes a single vertex, and each tile therefore requires 3 rows of data to describe. These 3 rows have different values of Petal Length, and there is not a 1:1 correspondence between rows and tiles.
The obvious option is to average the Petal Length of the three vertices, but it seems that ggforce does not have an option to interpolate the vertices this way. However, we can use the deldir package in the same way ggforce does to achieve this ourselves:
library(ggplot2)
library(deldir)
tri <- triang.list(deldir(iris$Sepal.Length, iris$Sepal.Width))
do.call(rbind, lapply(seq_along(tri),
function(x) {
data.frame(Sepal.Length = tri[[x]]$x, Sepal.Width = tri[[x]]$y,
Petal.Length = mean(iris$Petal.Length[tri[[x]]$ptNum]),
tri = x)
})) |>
ggplot(aes(Sepal.Length, Sepal.Width)) +
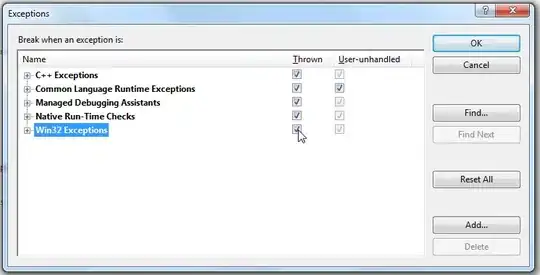
geom_polygon(aes(fill = Petal.Length, group = tri))
Additional
To gradient fill your triangles, probably best to draw blank triangles over a 2D interpolation:
library(interp)
library(ggforce)
interp(iris$Sepal.Length, iris$Sepal.Width, iris$Petal.Length,
duplicate = "mean", nx = 1000, ny = 1000) |>
interp2xyz() |>
as.data.frame() |>
setNames(names(iris)[1:3]) |>
ggplot(aes(Sepal.Length, Sepal.Width)) +
geom_raster(aes(fill = Petal.Length)) +
scale_fill_continuous(na.value = NA) +
geom_delaunay_tile(data = iris, fill = NA, color = "#00000050")
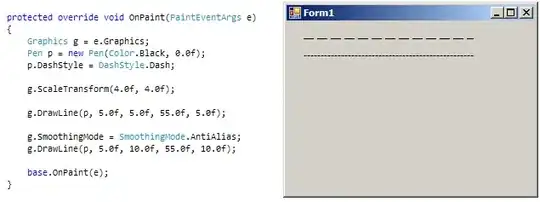
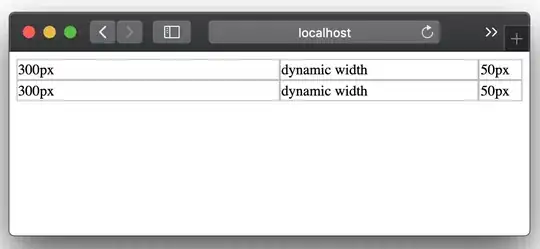 Now I would like to do a similar plot but with Delaunay triangulation, where the triangles are also filled like the polygons in the Voronoi plot above, however, I can't work out how to fill/color the triangles by a third variable
Now I would like to do a similar plot but with Delaunay triangulation, where the triangles are also filled like the polygons in the Voronoi plot above, however, I can't work out how to fill/color the triangles by a third variable