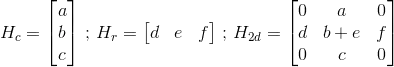Constrain a 3D mesh to not have overlapping triangles when projected in a specific plane

Question

I have a 3D polygon composed of points which are almost coplanar, vertically (which means the offset distances from those points which are not coplanar are orders of magnitude smaller than the distances between the points. They are due to numerical precision issue.).

I know the definition of the Euclidean plane of which they should be part of. But they are actually not part of it because of some numerical inaccuracies.

Is there a way, e.g. with Trimesh, to enforce a triangulation on these points so that the resulting triangles are never overlapping each other when seen from an orthogonal view which is perpendicular to the plane (said differently; when projected on the plane)?

#Python 3.10.6 (main, Nov  2 2022, 18:53:38) [GCC 11.3.0]
import numpy as np # version 1.24.0
import trimesh # version 3.17.1
from shapely import wkt
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

A = wkt.loads('''POLYGON Z ((
    3094228.563000001 2220858.2252000012 58.66020000015850,
    3094228.563000001 2220858.2252000012 62.31250000034925,
    3094231.731899999 2220851.7289999984 62.31250000034925,
    3094231.731899999 2220851.7289999984 20.79300000029616,
    3094228.083999999 2220859.2069999985 20.79300000029616,
    3094228.083999999 2220859.2069999985 58.66020000015850,
    3094228.563000001 2220858.2252000012 58.66020000015850))
''')
a = np.array(A.exterior.coords)
x, y, z = a[:,0], a[:,1], a[:,2]

cloud = trimesh.PointCloud(a)
mesh = cloud.convex_hull

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c='red', s=40)
ax.plot_trisurf(
    mesh.vertices[:,0],
    mesh.vertices[:,1],
    Z=mesh.vertices[:,2],
    triangles=mesh.faces,
    shade=True,
)
ax.view_init(azim=47, elev=3, roll=0)
plt.show()

But the resulting mesh seems to have overlapping triangles (it glitters when I rotate the plot):

(note that one of the points is not shown in this figure because it is somewhere "inside" the triangles soup in the top right part)
(I also only want to keep those triangles which are inside the initial polygon, which is concave, but this worth an other question imho)