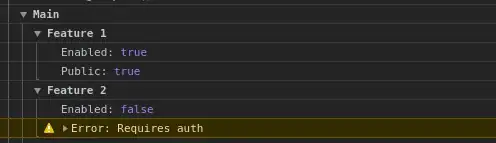
I have to draw a graph y = cos(x2+x+1) interval: [-π/2,π/2]. I have the graph without the interval, just making calculations with the screen resolution 320 x 200.
This is my code so far:
;------------------------------------------------------------------------
%include 'yasmmac.inc'
org 100h
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
section .text ; code starts here
startas:
call procSetGraphicsMode
xor di, di ; Y
.vertical:
mov si, 160 ; X
mov cl, 15 ; Color
call procPutPixel
inc di
cmp di, 199 ; MaxY
jbe .vertical
xor si, si ; X
.horizontal:
mov di, 100 ; Y
mov cl, 15 ; Color
call procPutPixel
inc si
cmp si, 319 ; MaxX
jbe .horizontal
; y = di
; x = si
mov si, 320
mov di, 100
xor si, si ; X
fninit
fld1 ; CONST 1
.loop:
mov [valueX], si ; X
fild word [valueX] ; st0 = X
fmul st0 ; st0 = X^2
fiadd word [valueX] ; st0 = X^2 + X
fadd st0, st1 ; st0 = X^2 + X + 1
fcos ; st0 = cos(X^2 + X + 1) [-1,+1]
fimul word [scaleY]
fistp word [y] ; {-1,0,+1}
mov di, 100 ; Y
add di, [y] ; -> Y={99,100,101}
mov cl, 4 ; Color
call procPutPixel
inc si
cmp si, 319
jbe .loop
call procWaitForEsc
exit
%include 'yasmlib.asm'
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
section .data ; data
R:
dd 50.0
value1:
dd 0.0
value2:
dd 0.0
value3:
dd 1.0
valueX:
dw 0
scaleY:
dw 60
x:
dw 0
y:
dw 0
N:
dw 360
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
section .bss
This code section draws a coordinate plane and the graph, not in the given interval [-π/2,π/2]. 
What I want the program to do is to draw that interval within the interval [-π/2,π/2]. So it would look something like this: 
I need somehow scale my X so that the graph would be within the intervals.
I was thinking to make the starting point of X in the center (160), but I can't imagine, how to move to both sides (negative - towards -π/2 and positive - towards π/2). I have tried to explain that as clearly as I could.
If more information is needed, I will try to edit the question.