Matrix are weird animals. They let you take a bunch of shapes and translate, rotate or scale them all at once, but only through playing with the coordinate system, which implies that the way you draw the shapes that you'll process will have a huge impact on how they react.
This is your plane on a neutral grid (by which I mean that globalX and globalY are 0):

Every square on this grid has a 20 pixels side. As you can see, your plane is far from the [0, 0] point, which is the start of the coordinate system it's drawn into. Also, when you modify it's coordinates, you're doing it through modifying it's coordinates, as we can see on this line of code:
void dessinerAvion(int x, int y)
The problem here is that applying a geometric transformation to an object with these coordinates can be counterintuitive. To simplify the matter, imagine the whole coordinate system that the plane use as if it was an image, like a png. The top left of the image is the [0, 0] point. When you change the plane's y coordinates for a higher number, your png image gets taller. If you change the x coordinate of the plane for a bigger number, the png image gets wider. You get the general idea.
When you apply a rotation to the plane, it's the entire 'png image', the entire coordinate system, that gets rotated. It's the same for any other transformation, too. Now, experimentally, look at what happens if I do this:
for(float i=0; i<20; i+=1) {
pushMatrix();
rotate(PI/i);
dessinerAvion(0, 0);
popMatrix();
}
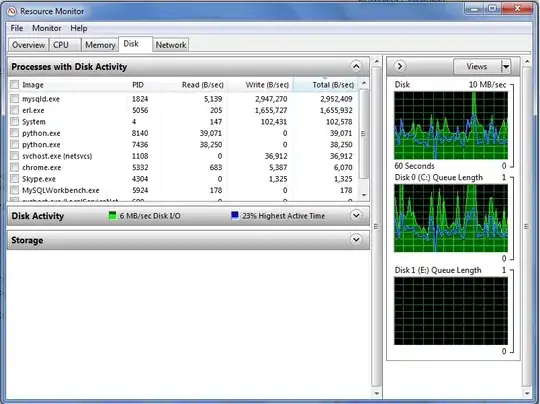
As you can see, the plane isn't rotating on itself. It's the whole coordinate system that rotates, pivoting on the [0, 0] point, and it brings the plane with itself. That's the deal with matrix: they keep a lot of geometry waaay more simple, but you have to work accordingly.
Which brings me back to the previous point: you're updating the coordinates where you draw the plane. Then you use a matrix. Your updated plane will rotate in an unexpected way because you apply 2 different logic to your transformations: on one hand you modify coordinates (which is fine), while on the other you apply a transformation on a matrix (which is fine too). The issue is to mix those without acknowledging their differences.
Honestly, unless you have a specific thing in mind, you shouldn't mix those to move a single object.
The obvious solution to the first part of this issue would be to translate the plane instead of moving it's coordinates:
void draw() {
background(255);
bouger(); // updating coordinates, this doesn't need to be in the matrix block
pushMatrix();
//tourner();
translate(globalX, globalY);
dessinerAvion(0, 0); // zero here as the translation is doing that part of the job now
popMatrix();
}
Now you should see... well, you should see no difference at all. That's normal. The real difference is not in how the sketch appears, but how it's processed behind the scenes. Now your plane is a static object on which we apply geometric transformations.
Now to the other part of your problem: animating an object. Well, to be honest the animation part is quite easy, but there's a lot of work to do beforehand, more precisely to fix the plane's original coordinates so they are easier to manage. Let me explain:
If you look at the first image where I show the plane without any geometric transformation, you'll notice that the left wing starts at about ~75 pixels from the 0 point, and that the nose of the plane is ~45 pixels away from the 0 on the y axis. Currently, that's the rotation's anchor point. If you want to rotate the plane in a gracious manner, you'll have to fix this. There are many ways to proceed, follow me.
Take notes, because for some reason very few people will explain in simple words how to rotate on an anchor point using a matrix.
To rotate a shape on a specific anchor point, you have to proceed as follow:
- pushMatrix
- translate to the shape's destination
- rotate
- draw the shape using [0, 0] as it's anchor point
- popMatrix
So if you want to rotate your plane on itself, thus deciding on an angle then moving it to it's destination before you draw the plane, you act as follow:
void draw() {
background(255);
// grid
stroke(0);
for (int i=0; i<height; i+=20) {
line(0, i, width, i);
}
for (int i=0; i<width; i+=20) {
line(i, 0, i, height);
}
pushMatrix();
translate(200, 200); // for the demonstration only
globalAngle--;
rotate(radians(globalAngle)); // I'm lazy and I don't want to do this in radians so I use degrees and convert them
dessinerAvion(-250, -200); // the center of the plane is the [250, 200] point. That's my anchor point.
popMatrix();
}
Which gives us this result:
Now, using the first translate, you can draw the plane wherever you want, and you can use the rotation to make it face any direction you want it to face.
Using these, it would be real easy to make the plane cross the screen back and forth:
void draw() {
background(255);
drawGrid();
// implementing the "u-turn"
globalY -= vitesse;
if (globalY < -200) {
globalX -= 200;
globalAngle = 180;
vitesse = -vitesse;
}
// drawing the sketch
pushMatrix();
translate(globalX, globalY);
rotate(radians(globalAngle));
dessinerAvion(-250, -200);
popMatrix();
}
Now, if we want to watch the plane turn, we have several options. You can rotate the plane frame by frame while plotting it's course. That's a good option. But I'm lazy, as previously stated, so instead I'll move the anchor point somewhere left of the plane and use it to rotate around it in a gracious manner:
void draw() {
background(255);
drawGrid();
pushMatrix();
translate(globalX, globalY);
tourner();
bouger();
dessinerAvion(0, -200); // this coordinate sets my anchor point
popMatrix();
}
void tourner() {
if (globalY < 300) { // starting the u-turn
vitesse = 0; // The plane won't move while it's rotating... except for the rotation itself
globalAngle--; // rotating counterclockwise 1 degree per frame
if (globalAngle<-180) { // u-turn completed
globalAngle = -180;
vitesse = -3;
}
}
rotate(radians(globalAngle));
}
I think that does it. I hope this helps. I'll lurk around in case you have questions about this answer.
Have fun!