The question says draw F(A,B,C,D)=∑(3,7,11,12,13). I derived A'B'CD+ABC'. I am trying to draw it using two inverters and 5 2:1 multiplexers but i couldn't connect the output to the separate components i wrote. I know the correct answer but i just couldn't understand it.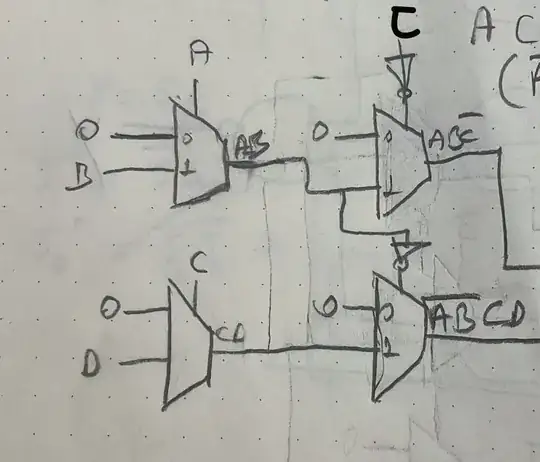
Why is the last mux connected to the 0 instead of 1 like we did all the other components? And why did they give 1 to 1 in mux in the answer?