3

I am trying to calculate the convolution of 

x(t) = 1, -1<=t<=1
x(t) = 0, outside

with itself using the definition.

http://en.wikipedia.org/wiki/Convolution

I know how to do using the Matlab function conv, but I want to use the integral definition. My knowledge of Matlab and WolframAlpha is very limited.

Amro
  • 123,847
  • 25
  • 243
  • 454
Bruno Calza
  • 2,732
  • 2
  • 23
  • 25
  • Using the convolve function in WolframAlpha, it becomes very simple: convolve[Piecewise[{{1, -1 <= x <= 1}}, 0],Piecewise[{{1, -1 <= x <= 1}}, 0],x,t] – Bruno Calza Oct 03 '11 at 14:25

3 Answers3

8

I am still learning Mathematica myself, but here is what I came up with..

First we define the piecewise function (I am using the example from the Wikipedia page)

f[x_] := Piecewise[{{1, -0.5 <= x <= 0.5}}, 0]

piecewise_function

Lets plot the function:

Plot[f[x], {x, -2, 2}, PlotStyle -> Thick, Exclusions -> None]

function_plot

Then we write the function that defines the convolution of f with itself:

g[t_] = Integrate[f[x]*f[t - x], {x, -Infinity, Infinity}]

convolution_integral

and the plot:

Plot[g[t], {t, -2, 2}, PlotStyle -> Thick]

convolution_plot

EDIT

I tried to do the same in MATLAB/MuPad, I wasn't as successful:

f := x -> piecewise([x < -0.5 or x > 0.5, 0], [x >= -0.5 and x <= 0.5, 1])

func_def

plot(f, x = -2..2)

func_plot

However when I try to compute the integral, it took almost a minute to return this:

g := t -> int(f(x)*f(t-x), x = -infinity..infinity)

convolution

the plot (also took too long)

plot(g, t = -2..2)

convolution_plot

Note the same could have been done from inside MATLAB with the syntax:

evalin(symengine,'<MUPAD EXPRESSIONS HERE>')
Amro
  • 123,847
  • 25
  • 243
  • 454
  • It's probably better to use `g[t_] = Integrate[f[x]*f[t - x], {x, -Infinity, Infinity}]` rather than `g[t_] := Integrate[f[x]*f[t - x], {x, -Infinity, Infinity}]` (ie replace `SetDelayed` by `Set`), so as to avoid recomputing the symbolic integral each time as currently happens (this is grossly inefficient). This makes a single evaluation of `g[5]` around 1500 times faster on my machine. – acl Sep 14 '11 at 18:13
  • You could use `UnitBox[x]` instead of the somewhat complexer `Piecewise` function. – Sjoerd C. de Vries Sep 14 '11 at 19:11
  • 3
    +1. To protect your definition against cases when `t` has already been defined and has a value, you could insert `Clear[t]` prior to `g[t]=...`, or wrap your definition in `Block`, like `Block[{t},g[t_]=...]`. This wasn't an issue with your original definition based on `SetDelayed` (`:=`), but becomes more important when you use immediate assignments (`Set`), as rightly suggested by @acl. I considered a very similar example here: http://www.mathprogramming-intro.org/book/node381.html – Leonid Shifrin Sep 14 '11 at 21:13
  • Probably MuPAD took so long because you did use the piecewise function... Try using rectangular pulses and the equations of both segments, it gets faster. – Andry Apr 12 '13 at 09:11
  • @Andry: definitely worth a try, I admit my MuPAD knowledge is also very limited. Sjoerd did suggest using `UnitBox` instead of a piecewise function.. – Amro Apr 12 '13 at 22:36
  • 1
    @Amro: :) The function you need is called `rectpulse` (http://www.mathworks.com/help/symbolic/mupad_ref/rectpulse.html) which is a shortcut for `rectangularPulse` (http://www.mathworks.com/help/symbolic/mupad_ref/rectangularpulse.html). – Andry Apr 13 '13 at 07:50
  • When you use a function defined with `piecewise` no problem if you use it just to calculate values. But when you try to use it and feed such a function to other mupad functions, it gets terrible. Slower and sometimes you even fail calculations. Recently I discovered this myself, believe me, try a different definition :) – Andry Apr 13 '13 at 07:52
1

Mathematica actually has a convolve function. The documentation on it has a number of different examples:

http://reference.wolfram.com/mathematica/ref/Convolve.html?q=Convolve&lang=en

Searke
  • 779
  • 3
  • 3
0

I don't know much about Mathematica so I can only help you (partially) about the Matlab part.

To do the convolution with the Matlab conv functions means you do it numerically. What you mean with the integral definition is that you want to do it symbolically. For this you need the Matlab Symbolic Toolbox. This is essentially a Maple plugin for Matlab. So what you want to know is how it works in Maple.

You might find this link useful (wikibooks) for an introduction on the MuPad in Matlab.

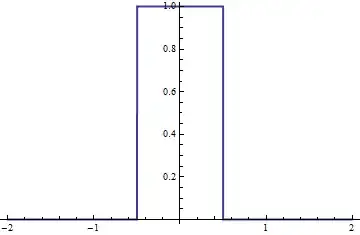
I tried to implement your box function as a function in Matlab as

t = sym('t')
f =  (t > -1) + (t < 1) - 1

However this does not work when t is ob symbolic type Function 'gt' is not implemented for MuPAD symbolic objects.

You could declare f it as a piecewise function see (matlab online help), this did not work in my Matlab though. The examples are all Maple syntax, so they would work in Maple straight away.

To circumvent this, I used

t = sym('t')
s = sym('s')
f = @(t) heaviside(t + 1) - heaviside(t - 1)

Unfortunately this is not successful

I = int(f(s)*f(t-s),s, 0, t)

gives

Warning: Explicit integral could not be found.

and does not provide an explicit result. You can still evaluate this expression, e.g.

>> subs(I, t, 1.5)

ans =
1/2

But Matlab/MuPad failed to give you and explicit expression in terms of t. This is not really unexpected as the function f is discontinuous. This is not so easy for symbolic computations.

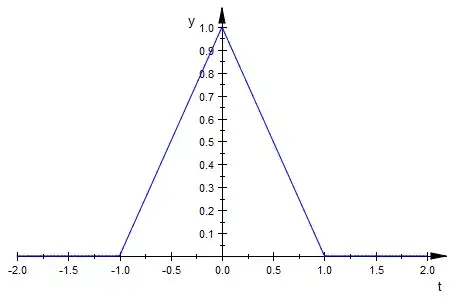
Now I would go and help the computer, fortunately for the example that you asked the answer is very easy. The convolution in your example is simply the int_0^t BoxFunction(s) * BoxFunction(t - s) ds. The integrant BoxFunction(s) * BoxFunction(t - s) is again a box function, just not one that goes from [-1,1] but to a smaller interval (that depends on t). Then you only need to integrate the function f(x)=1 over this smaller interval.

Some of those steps you would have to to by hand first, then you could try to re-enter them to Matlab. You don't even need a computer algebra program at all to get to the answer.

Maybe Matematica or Maple could actually solve this problem, remember that the MuPad shipped with Matlab is only a stripped down version of Maple. Maybe the above might still help you, it should give you the idea how things work together. Try to put in a nicer function for f, e.g. a polynomial and you should get it working.

H. Brandsmeier
  • 957
  • 5
  • 19