2

When studying the literature on physics engines, I've noticed that almost every physics engine uses semi-implicit Euler. The basic implementation of this uses the following two equations:

v_{n+1} = v_n + a_n * dt (eq1)

x_{n+1} = x_n + v_{n+1} * dt (eq2)

However since we have the second order derivative information of the position anyways, why don't we use a Taylor expansion? This would result in the following two equations:

v_{n+1} = v_n + a_n * dt (eq3)

x_{n+1} = x_n + v_n * dt + 1/2 * a_n * dt^2 (eq4)

If we compare these two sets of equations (subs eq1 in eq2), then you can see that we actually have an order difference:

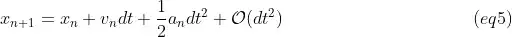
x_{n+1} = x_n + v_n * dt + a_n * dt^2 + O(dt^2) (eq5)

x_{n+1} = x_n + v_n * dt + 1/2 * a_n * dt^2 + O(dt^3) (eq6)

To verify a bit whether an implementation like this would be possible, I've also quickly skipped through some of the integrators source code of MuJoCo, in which I did not see an immediate drawback of actually implementing this method (only a rather small extra computation cost for separately adding that extra term).

So my question remains: Why are physics engines not using a Taylor expansion for the position?

Timo Stienstra
  • 56
  • 5

2 Answers2

1

As @saranTunyasuvunakool already mentioned it is really about semi-implicit Euler being symplectic, which is preferable for Hamiltonian systems. A really good post explaining this further is: https://scicomp.stackexchange.com/a/29154/44176

Timo Stienstra
  • 56
  • 5
0

I did not see an immediate drawback of actually implementing this method (only a rather small extra computation cost for separately adding that extra term).

I think you too easily discount the importance of the "small extra computation cost". The first technique you describe requires two additions and two multiplications per position update. The second requires two additions and four multiplications,* for 50% more arithmetic operations.

In practice, the cost increase actually observed would probably be less than 50%, both because position computations, though prominent, are not the only ones performed by the engine, and also because the processor might not need to perform all the multiplications and additions as discrete operations. Nevertheless, I see no reason to expect the observed cost increase to be so low as to be negligible. The typical physics engine cares very much about how many frames it can crank out per unit time, so as long as the resulting simulation is sufficiently realistic, I would expect the cheaper alternative to be chosen every time.

*Supposing that the time step is not constant, but as a practical matter, that's a necessary assumption for most engines.

John Bollinger
  • 160,171
  • 8
  • 81
  • 157
  • The additional computation from that extra term is negligible amount compared to the cost of other parts of the physics pipeline (in particular collision detection and constraint resolution). The reasoning behind integrator choice is mathematical. I'll try to find time to write up something, but the short answer is that semi-implicit Euler is symplectic (Hamiltonian-preserving) for certain systems. – Saran Tunyasuvunakool Oct 07 '22 at 16:44
  • @SaranTunyasuvunakool is correct, but that doesn't mean that your proposal isn't valuable. In practice the only way to find out is to try it for several types of dynamical systems. Please post here if you get around to trying it and learn something from you experiments (both positive and negative results would be interesting, AFAIC) – yuval Oct 08 '22 at 12:36
  • Computational maths uses floats that are only an approximations and are very prone to error. "semi-implicit Euler" helps reduce problems by damping the error. This allows the code to use greater time steps (less iterations) while maintaining a stable simulation, saving many more CPU cycles than just those in the equation. – Blindman67 Oct 11 '22 at 14:25
  • @Blindman67, if you were to tell me that semi-implicit Euler is stable because the *systematic* errors in the form of the instantaneous equations of motion tend to cancel out, then I would be interested in hearing more. I would also be interested in hearing more about why that affords larger step sizes than directly reducing the systematic error would do. However, inasmuch as I expect the systematic errors to be several orders of magnitude larger than FP rounding error, I find it hard to credit dealing with the latter as a plausible explanation for prefering implicit Euler. – John Bollinger Oct 11 '22 at 14:43