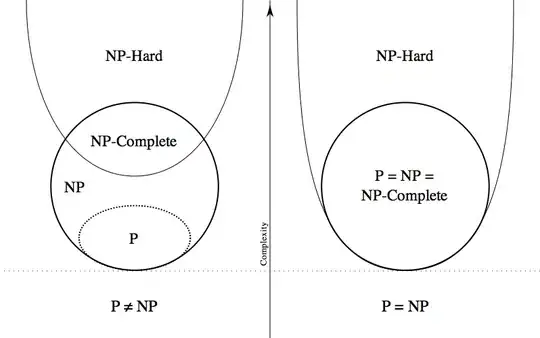
The definition of NP-complete is
A problem is NP-complete if
- it belongs to class NP
- all the other problems in NP polynomially transform to it
So, if all other problems in NP transform to an NP-complete problem, then does that not also mean that all NP problems are also NP-complete? What is the point of classifying the two if they are the same?
In other words, if we have an NP problem then through (2) this problem can transform into an NP-complete problem. Therefore, the NP problem is now NP-complete, and NP = NP-complete. Both classes are equivalent.
Just trying to clarify this up for myself.