I'm trying to emulate an animation effect in code (almost any language would do as it appears to be math rather than language). Essentially, it is the emulation of a mass-spring system. I've been looking at WPF/Silverlight's ElasticEase and this appears to be pretty close to what I'm looking for, but not quite.
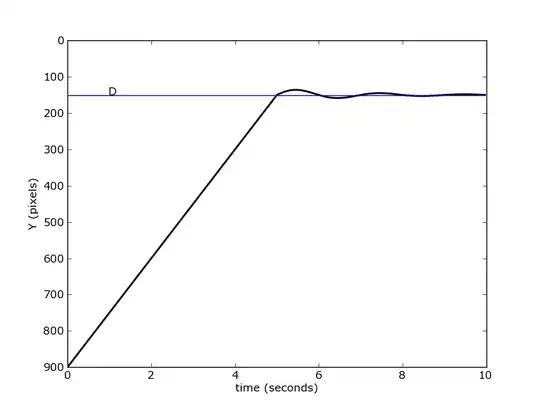
First of all, here's what I'm looking for - an object, travelling a certain number of seconds, hitting a location and immediately slowing down to ocsillate for a certain number of seconds to rest at the same point where damping was applied. So to visualize this, let's say I have a 600w/900h canvas and I have an square that begins to animate from 900px to 150px in a TranslateTransform.Y. It takes 4 seconds to reach 150px height (187.5px per second), at which stage it immediated gets damped and only travels about 35px more for 0.4 seconds (87.5px per second) to 115px height, then rebounds down for 1 second to 163px height (48px and 48px per second) and then rebounds back up to 146px (17px and 17px per second) and so on until the ocillations slow it to its final resting place of 150px. The ocillation period is 16 seconds.
The example I described above is the top left blue rectangle here:

Here's what I will know in advance - the pixel distance and number of seconds it takes to get from point A to point B, the number of seconds for ocillation. Things like mass don't seem to matter.
I've tried ElasticEase and the issue seems to be that I can't get the object to travel with no easing for 4 seconds and then "bounce" for the next 16 seconds. The .Springiness is also always way too much, even if I set it to be a really high number like 20.
ILSpy show's its function as:
protected override double EaseInCore(double normalizedTime)
{
double num = Math.Max(0.0, (double)this.Oscillations);
double num2 = Math.Max(0.0, this.Springiness);
double num3;
if (DoubleUtil.IsZero(num2))
{
num3 = normalizedTime;
}
else
{
num3 = (Math.Exp(num2 * normalizedTime) - 1.0) / (Math.Exp(num2) - 1.0);
}
return num3 * Math.Sin((6.2831853071795862 * num + 1.5707963267948966) * normalizedTime);
}
I've included 2 videos and and an Excel file in a zipped folder on DropBox. I guess this question will be more of a work-in-progress as folks ask more clarifying questions.
(DISCLAIMER: I don't know what I'm talking about when it comes to much of this stuff)