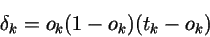hash function for a set of 2d curves

Question

I am looking for some spatial hashing algorithms that can hash a list of 2d curves (bezier splines) and have following properties:

1. Tolerance: since control points are expressed in float3 (where z is always 0), I need some kind of threshold to ensure spatially similar curves results in the same hash.

2. Simple: I intend to implement it in a real-time node-based system running on CPU, this system only offers integer/float/vector math operations (no bitwise ops, no loops), so the fewer steps the merrier for me.

3. Output hash in Int32: again this is limited by my node-based system.

4. OK collision rate: it is perfectly fine to have collisions, but it should be better than a modulo over x and y.

Having said that, here is my actual problem:

• Imagine a simple 2d polygon;

• We will randomly (procedurally) generated grid lines that cut through this polygon.

• We later randomly (procedurally) slightly warp these edges, and represent them as bezier splines.

• Now we want to hash them, so that if we later add/remove/modify some of these lines (now splines), the system know which ones have changed and which ones haven't.

(It is possible to ignore the warp step and simply encode the start and end points of each line, but ideally we should be able to identify 2 line with same start/end points but has different warp factor.)

I have done some research on this topic, but are unsure what kind of hashing algorithm I should look into, a few related terms including:

• Geometric hashing
• Perceptual hashing
• Locality-sensitive hashing

In summary, can you help me on these 2 questions:

1. Which properties should I encode in my cases?

2. Any simple hashing functions that seem suitable for my use cases?