How to calculate the positions of new points after rotating the image around arbitrary axis

Question

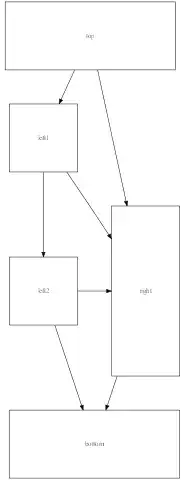
Having a dataset of aligned objects, I would like to augment it by applying random rotations with the axis at the center of the object. Below is the rotation representation (left original, right image rotated around the point (xc, yc). for rotation, I have used the following logic:

import cv2
import random
image_source = cv2.imread('sample.png')
height, width = image_source.shape[:2]
random_angle = random.uniform(90, 90)
yolo_annotation_sample = get_annotation() # this function retrieves yolo annotation
label_id, xc, yc, object_width, object_height = yolo_annotation_sample # e.g. 4, 0.0189, 0.25, 0.0146, 0.00146

center_x = width * xc
center_y = height * yc
left = center_x - (width * object_width) / 2
top = center_y - (height * object_height) / 2
right = left + width * object_width
bottom = top + height * object_height

M = cv2.getRotationMatrix2D((cx, cy), random_angle, 1.0)
image_rotated = cv2.warpAffine(image_source, M, (width, height))
# logic for calculating new point position (doesn't work)
x1_y1 = np.asarray([[left, top]]) 
x1_y1_new = np.dot(x1_y1, M)
x2_y2 = np.asarray([[right, top]]) 
x2_y2_new = np.dot(x2_y2, M)
x3_y3 = np.asarray([[right, bottom]]) 
x3_y3_new = np.dot(x3_y3, M)
x4_y4 = np.asarray([[left, bottom]]) 
x4_y4_new = np.dot(x4_y4, M)

Does anyone know how to recalculate the point(s) after rotating around the arbitrary point as shown above?

look up the docs for `cv::warpAffine`. see the "see also" section to learn about the function that works on points instead of images. — Christoph Rackwitz, Aug 25 '22 at 09:02
`np.dot()` is a dot product, not a matrix multiplication. It cannot be used to do rotations. The operator for matrix multiplication is `@`, or `np.matmul()` — Colim, Aug 25 '22 at 15:23
close enough. numpy's `dot` has some extended behavior. for readability I too would recommend `@`. *"If both a and b are 2-D arrays, it is matrix multiplication, but using matmul or a @ b is preferred."* — Christoph Rackwitz, Aug 25 '22 at 15:48
[cv2.transform] (https://docs.opencv.org/4.6.0/d2/de8/group__core__array.html#ga393164aa54bb9169ce0a8cc44e08ff22) should work. Usage [example](https://stackoverflow.com/questions/44378098/trouble-getting-cv-transform-to-work). Multiply M by (x, y) is not going to work. It may work with [Homogeneous Coordinates](https://en.wikipedia.org/wiki/Homogeneous_coordinates#): Add a third row `[0, 0, 1]` to matrix `M`, multiply `M` by column vector `[x, y, 1]` (and ignore the third output element that is always `1`). — Rotem, Aug 25 '22 at 19:12
`transform` itself adds a dimension when needed. it's supposed to work here. -- `perspectiveTransform` deals with the homogeneous stuff (division), but you don't need that for affine transformations. -- and then there's `convertPointsFromHomogeneous` and `convertPointsToHomogeneous`, if you need to do something special — Christoph Rackwitz, Aug 25 '22 at 19:22

score 2 · Accepted Answer · answered Aug 26 '22 at 10:20

Use cv2.transform(points, M). Points with shape: (4, 1, 2). Full code:

import cv2
import random
import numpy as np

image_source = cv2.imread('sample.png')
height, width = image_source.shape[:2]
random_angle = 40 #random.uniform(90, 90)
yolo_annotation_sample = (4, 0.6189, 0.25, 0.246, 0.0846) # this function retrieves yolo annotation
label_id, xc, yc, object_width, object_height = yolo_annotation_sample

center_x = width * xc
center_y = height * yc
left = center_x - (width * object_width) / 2
top = center_y - (height * object_height) / 2
right = left + width * object_width
bottom = top + height * object_height

cx, cy = width / 2, height / 2
M = cv2.getRotationMatrix2D((cx, cy), random_angle, 1.0)
image_rotated = cv2.warpAffine(image_source, M, (width, height))
# logic for calculating new point position (doesn't work)
bbox_points = [[left, top], [right, top], [right, bottom], [left, bottom]]
bbox_points = np.array(bbox_points).reshape((-1,1,2))
rotated_points = cv2.transform(bbox_points, M) # what you need

cv2.polylines(image_source,[bbox_points.astype(int)],True,(255,100,0), 10)
cv2.polylines(image_rotated,[rotated_points.astype(int)],True,(255,100,0), 10)

cv2.imshow("orig", image_source)
cv2.imshow("rotated", image_rotated)
cv2.waitKey()

Thanks, I was recalculating bounding boxes after rotating the base image and thought there had to be a way to rotate the list of boxes to follow the image. I was able to adapt your solution to my problem. — MattD, Dec 20 '22 at 20:16

score -1 · Answer 2 · answered Aug 25 '22 at 11:58

Look at [https://en.wikipedia.org/wiki/Transformation_matrix][1]

Once I tried to calculate it myself:

class rotm :
 '''set up rotation matrix'''
 def __init__(self,axis,angle,unit="radians") :   
  self.m = scipy.zeros((4,4),scipy.float128)
  if unit=="radians" :
   angler = angle
  else :
   angler = math.radians(angle)
  pass
  if axis=='x' :
   self.m[0][0]=1.0
   self.m[1][1]=math.cos(angler)
   self.m[2][2]=self.m[1][1]
   self.m[3][3]=1.0
   self.m[1][2]=-math.sin(angler)
   self.m[2][1]=-self.m[1][2]
  elif axis=='y' :
   self.m[0][0]=math.cos(angler)
   self.m[1][1]=1.0
   self.m[2][2]=self.m[0][0]
   self.m[3][3]=1.0
   self.m[0][2]=math.sin(angler)
   self.m[2][0]=-self.m[0][2]
  elif axis=='z' :
   self.m[0][0]=math.cos(angler)
   self.m[1][1]=self.m[0][0]
   self.m[2][2]=1.0
   self.m[3][3]=1.0
   self.m[0][1]=-math.sin(angler)
   self.m[1][0]=-self.m[0][1]
  pass         
 pass
 def fPrint(self) :
  '''auxiliary function: print transformation matrix '''      
  print(self.m)   
 pass     
pass #end of rotm class

that wasn't the question. OP already has an affine transformation matrix. — Christoph Rackwitz, Aug 25 '22 at 14:07
As it’s currently written, your answer is unclear. Please [edit] to add additional details that will help others understand how this addresses the question asked. You can find more information on how to write good answers [in the help center](/help/how-to-answer). — Community, Aug 30 '22 at 14:04

How to calculate the positions of new points after rotating the image around arbitrary axis

2 Answers2