I'm trying to solve the famous coin change problem using the naive recursive solution (I'll use this as a blueprint before adding memoization or tabulation).
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money. Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1. You may assume that you have an infinite number of each kind of coin.
My first attempt at a solution is below.
def coinChange(self, coins: List[int], amount: int) -> int:
if amount < 0:
return -1
min_choices = float('inf')
def coinChangeHelper(coins, amount):
if amount < 0 or (amount > 0 and not coins):
return -1
elif amount == 0:
return 0
min_choices = float('inf')
choice1 = 1 + coinChangeHelper(coins, amount - coins[0])
if choice1 > 0:
min_choices = min(min_choices, choice1)
choice2 = 1 + coinChangeHelper(coins[1:], amount)
if choice2 > 0:
min_choices = min(min_choices, choice2)
return min_choices
return coinChangeHelper(coins, amount)
This solution fails on the input [1,2,5] (coins), 11 (amount), returning 5 when the answer should be 3 (5->5->1). I've tried to draw out the recursive tree below to debug why my solution doesn't work. 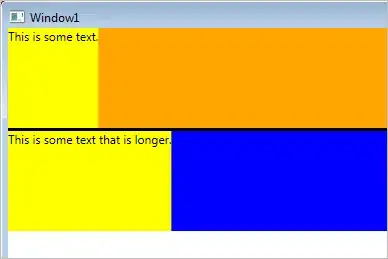
I then came up with another solution that works, copied below.
def coinChange(self, coins: List[int], amount: int) -> int:
def coinChangeHelper(coins, amount):
if amount < 0:
return -1
elif amount == 0:
return 0
min_choices = float('inf')
for coin in coins:
choices = 1 + coinChangeHelper(coins, amount - coin)
if choices > 0:
min_choices = min(min_choices, choices)
return min_choices
result = coinChangeHelper(coins, amount)
return -1 if result == float('inf') else result
I tried drawing the recursive tree for this solution and it seems more correct to me since at each recursive call, I still have all the coins to choose from. Can anyone explain why my first solution is wrong? The idea behind my first incorrect solution was by following this psuedocode
min_coins = current cost + min(cost without using this coin, cost using this coin)