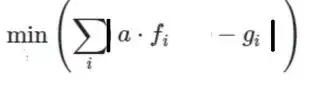-2

I've an absolute error loss function of the following form,

enter image description here

This function is used to scale the set of data points lying on a curve f to the target curve g.

I am trying to minimize the following objective function and the constraints are below

min: sum_i u_i
s.c.
f_i * a - u_i <= g_i
-f_i * a - u_i <= -g_i

I tried the following in MATLAB

% Loss Function (absolute error loss)
% input curves
scale =  1.5;
x1 = [0,4,6,10,15,20]*scale;
y1 =  [18,17.5,13,12,8,10];
x2 = [0,10.5,28]*scale;
y2= [18.2,10.6,10.3];

% y2 is the target function and y1 is the function to be shifted
f = y1;
g = interp1(x2,y2,x1);

% linprog inputs
% x = linprog(f,A,b)
% i = 1:length(x1)
A = [fi - 1; -fi -1];
x = [a ui];
b = [gi -gi];

% obj = sum_i u_i (function to minimize)
% solve system

I am not sure how to set this up and solve this system in MATLAB's linprog

It will also be helpful if suggestions are given for implementing the same using the linprog function in scipy.

Suggestions will be really helpful.

Natasha
  • 1,111
  • 5
  • 28
  • 66

1 Answers1

1

@Natasha. I hope I understood the question correctly and this is about finding the scale factor a for the function f which best approximates the function g in the least absolute deviation sense. If yes, then following remarks before I share some code:

  1. I placed the variable scale at another place in the code to see better whether the implementation is working correctly.
  2. Your idea about the implementation was very close. It was solely needed to write the linear constraints in matrix notation.
  3. Your objective function is essentially a quantile regression (at quantile 0.5). A quantile regression functions does not seem to exist as a standard Matlab function (so I indeed used linear programming). For Python, there is a quantile regression function in scikit-learn.

Matlab code:

clc; clear variables; close all;

%%%%%%%%%%%%
%%% DATA %%%
%%%%%%%%%%%%
% The constant "scale" is scaling the inputs rather than outputs. In your
% formulations this has little influence on the problem. I have placed the
% scaling on the output. The function g is now a factor 2 larger implying
% that we would expect a to be about 2 to match f to g.

x1 = [0, 4, 6, 10, 15, 20];
y1 =  [18, 17.5, 13, 12, 8, 10];

scale =  2;
x2 = [0, 10.5, 28];
y2= scale*[18.2, 10.6, 10.3];

% y2 is the target function and y1 is the function to be shifted
f = y1;
g = interp1(x2, y2, x1);
n = length(g);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% Linear programming problem %%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Let the vector x stack: a, u_1, ..., u_n
% fVector'*x should equal sum_i u_i
fVector = ones(n+1, 1);
fVector(1) = 0;
% Stack of linear constraints in matrix notation
A = [-f' -eye(n); f' -eye(n)];
b = [-g'; g'];

% Solver
LinProgOptions= optimoptions(@linprog,'algorithm','dual-simplex','display','none');
sol= linprog(fVector, A, b, [], [], [], [], [],LinProgOptions);
aSol = sol(1);

%%%%%%%%%%%%
%%% PLOT %%%
%%%%%%%%%%%%
figure(1)
plot(x1, f, 'LineWidth', 3)
hold on
plot(x1, g, 'LineWidth', 3)
plot(x1, aSol*f, 'LineWidth', 3)
hold off
legend('original f', 'g (interpolation)', 'a*f')

Python alternative:

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import linprog
from scipy import interpolate
from sklearn.linear_model import QuantileRegressor

############
### DATA ###
############
x1 = np.array([0, 4, 6, 10, 15, 20])
y1 =  np.array([18, 17.5, 13, 12, 8, 10]);

scale = 2
x2 = np.array([0,10.5,28])
y2= scale*np.array([18.2,10.6,10.3]);

# y2 is the target function and y1 is the function to be shifted
f = y1;
InterPolationFunction = interpolate.interp1d(x2, y2)
g = InterPolationFunction(x1)
n = len(g)

#######################################
### Solution 1: Quantile regression ###
#######################################
QuantileReg = QuantileRegressor(quantile=0.5, fit_intercept=False).fit(f.reshape(-1, 1), g)
aSol1 = QuantileReg.coef_[0]
print(aSol1)

######################################
### Solution 2: Linear programming ###
######################################
# Let the vector x stack: a, u_1, ..., u_n
# fVector'*x should equal sum_i u_i
fVector = np.ones((n+1,1))
fVector[0] = 0

# Stack of linear constraints in matrix notation
A = np.zeros( (2*n,(n+1)) )
A[0:n,0] = -f.T
A[n:(2*n),0] = f.T
A[0:n, 1:(n+1)] = -np.eye(n)
A[n:(2*n), 1:(n+1)] = -np.eye(n)
b = np.vstack( (-g.reshape(n,1),g.reshape(n,1)) )

# Solver
LinprogOutput = linprog(fVector, A_ub=A, b_ub=b)
aSol2 = LinprogOutput.x[0]
print(aSol2)

############
### PLOT ###
############
plt.figure()
plt.plot(x1, f, label = "original f")
plt.plot(x1, g, label = "g (interpolation)")
plt.plot(x1, aSol1*f, label = "a*f")
plt.legend()
plt.show()
Hanno Reuvers
  • 606
  • 3
  • 9